链式回转弹仓刚柔耦合动力学建模及特性分析

刘太素; 尹强; 李勇; 张云添

doi:10.12382/bgxb.2024.0698

PDF(8140 KB)

兵工学报 ›› 2024, Vol. 45 ›› Issue (11) : 4133-4144. DOI: 10.12382/bgxb.2024.0698

链式回转弹仓刚柔耦合动力学建模及特性分析

作者信息 +

Rigid-flexible Coupling Dynamic Modeling and Characteristics Analysis of a Rotational Chain Magazine

Author information +

本文二维码

文章历史 +

摘要

考虑到装填系统轨道输送链具有链节大、负载大、速度大的特殊性,提出一种基于相对坐标法和板单元离散方式的刚柔耦合动力学建模方法。利用邻接体的相对运动关系推导出运动学方程及体坐标与铰坐标的转化关系,建立广义坐标为独立铰坐标的动力学方程。利用有限元方法,基于板单元理论将链节和弹筒离散化,以链节为例建立单个链节的刚柔耦合动力学方程,随后通过刚-柔运动约束形式,利用增广方程形式,建立轨道输送链系统的刚柔耦合动力学方程。基于此方法,建立某弹仓(闭式轨道输送链)轨道输送链和弹筒的刚柔耦合动力学方程,并在不同工况下将基于板单元离散的数值仿真与实验结果进行对比。基于建立的刚柔耦合动力学模型,分析弹仓传动构件支撑刚度、轨道间隙等因素对弹仓系统的影响。研究结果表明:数值仿真结果与实验结果的趋势基本一致;支撑刚度对系统动态响应的影响程度取决于动力系统的结构形式和受力形式;轨道间隙的变化对系统的动态特性具有较大的影响,在工程应用中需要合理控制间隙;上下轨道错位对弹仓动态特性影响较大,需要合理控制加工装配精度。

Abstract

Considering the unique characteristics of the autoloader’s rail conveyor chain, such as large chain links, heavy load and high speed, a rigid-flexible coupljng dynamic modeling method based on the relative coordinate method and the plate element discretization method is proposed. The relative motion relationships of adjacent bodies are used to derive the kinematic equations and the transformation relationship between body coordinates and hinge coordinates, thereby establishing the dynamic equations with independent hinge coordinates as generalized coordinates. The finite element method is used to discretize the chain links and cartridge cases based on plate element theory. Taking the chain link as an example, the rigid-flexible coupling dynamic equations for a single chain link are established. Subsequently, the rigid-flexible coupling dynamic equations for the rail conveyor chain system are developed by applying the rigid-flexible motion constraints in the form of augmented equations. Based on this method, the rigid-flexible coupling dynamic equations of the rail conveyor chain and cartridge cases for a certain magazine are established. The numerical simulation based on plate element discretization is then compared with experimental results under different working conditions. The effects of factors such as the support stiffness of transmission components and rail clearance on the magazine system, are analyzed by using the proposed rigid-flexible coupling dynamic model. The research results indicate that the numerically simulated results are generally consistent with the experimental results. The influence of support stiffness on the system’s dynamic response depends on the structural form and force application of the power system. The change in rail clearance has a significant effect on the system’s dynamic characteristics, thus necessitating the reasonable control of clearance in engineering applications. The misalignment of the upper and lower rails has a considerable effect on the dynamic characteristics of the magazine, requiring the reasonable control of machining and assembly accuracy.

导出引用

刘太素 , 尹强 , 李勇 , 张云添. 链式回转弹仓刚柔耦合动力学建模及特性分析. 兵工学报. 2024, 45(11): 4133-4144 https://doi.org/10.12382/bgxb.2024.0698

LIU Taisu , YIN Qiang , LI Yong , ZHANG Yuntian. Rigid-flexible Coupling Dynamic Modeling and Characteristics Analysis of a Rotational Chain Magazine. Acta Armamentarii. 2024, 45(11): 4133-4144 https://doi.org/10.12382/bgxb.2024.0698

中图分类号： TJ301 (基础理论)

基金

国家自然科学基金项目(U2341269)

南京工程学院高层次人才科研基金项目(YKJ202104)

0 引言

弹药自动装填系统可以大幅度提升火炮在战场上的作战效能和生存率,凸显了其在火炮武器系统中的重要地位^[1-2]。作为弹药自动装填系统的重要组成部分,自动弹仓具有储弹、选弹的功能。由于构件尺寸误差、弹性变形、运动间隙以及外部环境扰动的影响,弹仓机构动作会出现松动、变形、卡滞等故障,导致弹丸实际到位与规定到位之间存在偏差,制约了自动装填系统的整体性能和可靠性提升。而在实际过程中,由于空间有限、工作环境复杂等因素限制,无法得到弹仓实装运行过程中特定关注位置的大量数据,从而制约了对弹仓故障的诊断与预测。通过仿真模型与试验相结合,可获得大量较准确的数据,从而有效地实现弹仓的故障诊断与可靠性提升设计。因此,建立准确的弹仓仿真模型,厘清关键因素对弹仓运动特性的影响规律,对弹仓的故障诊断和可靠性提升具有重要意义。

对于弹仓链传动建模及其特性分析方面,相关研究相对较少。文献[3-4]建立了弹仓的不确定性动力学仿真模型,并采用不同的优化策略辨识了模型中的不确定性未知参数,提高了模型的仿真精度。马超超等^[5]对重载链传动机构的传动误差进行了建模与分析,得到了链轮-链条配合间隙对最大总传动误差的影响规律,并通过优化的方法减小了传动误差。文献[6-7]开展了链式回转弹仓的精度控制研究,采用不同的控制算法提高了链式回转弹仓的到位精度。针对链传动输送机构的建模和运动特性,学者们开展了一系列研究,为弹仓链传动建模提供了一定的参考。文献[8-9]采用RecurDyn仿真软件对输弹机开式链传动进行了刚柔耦合动力学建模,分析了系统的动力学特性,为输送链的研究提供了一定的理论基础。文献[10]基于虚拟样机技术对输弹机开式齿形链进行了刚柔耦合动力学建模,并得到了齿形链的相关动力学特性。李伟等^[11]基于Adams软件建立了输弹机开式链的动力学模型,并分析了参数随机性对系统可靠性的影响。Li等^[12]建立了考虑间隙的输弹机构链传动仿真模型,并基于数据驱动的方法对关键参数进行了优化设计。Wei等^[13]基于弹仓动力学模型,提出了一种用于永磁同步电机驱动的链式弹仓全系统动力学估计方法,实现了弹仓中未知参数的准确估计。综合来看,弹仓输送链的建模方法基于传统链条的建模方法,一般有连杆等效法、集中参数法^[14-15]、多刚体动力学方法^[16⇓-18]。然而以上3种方法都有不足之处。连杆等效法便于实施,也可以反映弹仓输送链系统的局部特点,但无法建立完整的输送链模型;集中参数法能够反映链条的离散特性和链节的弹性变形,却无法考虑链节自身的转动惯量;多刚体动力学方法能够考虑构件完整的质量特性,却忽略了链节的弹性变形。大负载和大节距链是中大口径弹仓的结构特点,因此链节的柔性变形和转动惯量都是重点要考虑的因素。基于此,采用刚柔耦合动力学方法建立系统动力学方程是一个较好的选择。而且,考虑到弹仓链传动机构和弹筒三维实体柔性化建模造成的大量计算,Reissner-Mindlin中厚板理论^[19⇓-21]能够将三维实体单元简化为二维壳单元,保证精度的同时大大节约计算费用。基于刚柔耦合动力学方法,考虑影响弹仓运动的因素,即可建立弹仓刚柔耦合动力学模型,用以开展弹仓运动精度可靠性和故障诊断的研究。

本文针对弹仓轨道输送链链节大、负载大、速度大的特殊性,同时降低三维实体柔性化建模造成的大量计算,提出一种基于相对坐标法和中厚板理论离散方式的刚柔耦合动力学建模方法。基于Reissner-Mindlin中厚板理论建立链节和弹筒的柔性体模型,通过刚-柔运动约束的形式,结合相对坐标法建立弹仓刚柔耦合动力学模型,并通过实验验证了仿真模型的准确性。最后,基于准确的弹仓刚柔耦合动力学模型,分析了关键因素对弹仓动态特性的影响规律,从而为弹仓的故障诊断和可靠性提升提供了理论支撑。

1 某链式回转弹仓模型描述

考虑某弹仓的回转过程,弹仓主要由架体、电机、轨道、弹筒、链轮、链节和滚轮等主要零部件组成,示意图如图1所示。在电机的驱动下,带动链轮旋转,链轮带动滚轮在轨道内旋转,在滚轮与链节的闭式链传动作用下,带动弹盘旋转,完成回转动作。弹仓轨道链的拓扑关系如图2所示。

图1 弹仓结构组成

Fig.1 Composition of magazine structure

Full size|PPT slide

图2 弹仓主要结构拓扑关系

Fig.2 Main topological relationships of magazine structure

Full size|PPT slide

图2中,圆圈表示回转铰,三角形表示固定铰,菱形表示接触,点划线表示省略的滚轮与链节。由拓扑关系图可知,轨道是固连在大地上的,因此可将轨道的连体坐标系与惯性坐标系重合。组成链条的链节、滚轮、弹盘之间通过回转铰连接,形成闭式链传动机构。

主要构件的质量参数如表1所示。

表1 构件的质量、惯量参数

Table 1 Mass and inertia parameters of components

构件名称	质量/kg	惯量/(kg·m²)
构件名称	质量/kg	I_xx	I_yy	I_zz
链轮	16.629	2.00	2.00	1.82×10^-2
链节	0.152	1.93×10^-4	2.01×10^-4	9.73×10^-6
弹筒	8.58	0.791	0.807	3.11×10^-2
滚轮	5.35×10^-2	5.20×10^-6	5.20×10^-6	8.31×10^-6
弹丸	45.1	2.48	2.48	0.168

注:I_xx、I_yy、I_zz分别为绕x轴、y轴、z轴的转动惯量。

2 基于中厚板结构的链节力学模型

针对链节的结构特性,采用Reissner-Mindlin中厚板模型^[19⇓-21]方式进行建模,相对于实体模型,在相同精度的前提下,板模型描述的链节模型可以减小一定的计算量。

2.1 Reissner-Mindlin中厚板建模

通过1阶剪切变形理论,中厚板在笛卡尔坐标系中的位移可表示为以下形式:

u(x,y,z)=u₀(x,y)+zθ_y(x,y)

(1)

v(x,y,z)=v₀(x,y)-zθ_x(x,y)

(2)

w(x,y,z)=w₀(x,y)

(3)

式中:u(x,y,z)、v(x,y,z)、w(x,y,z)分别为x轴、y轴、z轴方向的位移;u₀、v₀和w₀为中面位移;θ_x和θ_y的方向分别指向x轴和y轴的正方向,如图3所示。图3中,a、b、t分别为板的长度、宽度、厚度。

图3 变形挠度和转角的方向

Fig.3 Direction of deformation deflection and angular displacement

Full size|PPT slide

由几何方程和式(1)~式(3),可得应变表达式为

ε=

\{\begin{array}{l} ε_{x x} \\ ε_{y y} \\ γ_{x y} \\ γ_{x z} \\ γ_{y z} \end{array}\}

\{\begin{array}{l} ε_{m} \\ 0 \end{array}\}

\{\begin{array}{l} ε_{b} \\ 0 \end{array}\}

\{\begin{array}{l} 0 \\ ε_{s} \end{array}\}

(4)

式中:ε_xx、ε_yy分别为x轴、y轴方向的正应变;γ_xy、γ_xz、γ_yz分别为xy、xz、yz平面的剪应变;ε_m、ε_b和ε_s分别为薄膜应变、弯曲应变和剪切应变,

ε_m=

\{\begin{array}{l} \frac{\partial u_{0}}{\partial x} \\ \frac{\partial v_{0}}{\partial y} \\ \frac{\partial u_{0}}{\partial y} + \frac{\partial v_{0}}{\partial x} \end{array}\}

,ε_b=

\{\begin{array}{l} \frac{\partial θ_{y}}{\partial x} \\ \frac{\partial θ_{x}}{\partial y} \\ \frac{\partial θ_{y}}{\partial y} - \frac{\partial θ_{x}}{\partial x} \end{array}\}

,ε_s=

\{\begin{array}{l} \frac{\partial w_{0}}{\partial x} + θ_{y} \\ \frac{\partial w_{0}}{\partial y} - θ_{x} \end{array}\}

(5)

基于1阶剪切板的假设,从能量原理的动态形式可推导出中厚板自由振动分析的弱形式为

\begin{array}{l} \int_{Ω} δ ε_{m}^{T} D_{m} ε_{m} d Ω + \int_{Ω} δ ε_{b}^{T} D_{b} ε_{b} d Ω + \\ \int_{Ω} δ ε_{s}^{T} D_{s} ε_{s} d Ω + \int_{Ω} δ d^{T} m \ddot{d} d Ω = 0 \end{array}

(6)

式中:Ω为板的体积;D_m为薄膜刚度本构系数;D_b为弯曲刚度本构系数;D_s为横向剪切刚度本构系数;δd为位移域d={

\begin{array}{l} u_{0} & v_{0} & w_{0} & θ_{x} & θ_{y} \end{array}

}^T的变分;m为含有密度ρ和厚度t的惯性矩阵;m、D_m、D_b和D_s的表达式分别为

m=ρ

[\begin{array}{l} t & 0 & 0 & 0 & 0 \\ 0 & t & 0 & 0 & 0 \\ 0 & 0 & t & 0 & 0 \\ 0 & 0 & 0 & \frac{t^{3}}{12} & 0 \\ 0 & 0 & 0 & 0 & \frac{t^{3}}{12} \end{array}]

(7)

D_m=

\int_{- t / 2}^{t / 2_{}}

D₀dz=tD₀

(8)

D_b=

\int_{- t / 2}^{t / 2_{}}

z²D₀dz=

\frac{t^{3}}{12}

D₀

(9)

D_s=

\int_{- t / 2}^{t / 2_{}}

κG

[\begin{array}{l} 1 & 0 \\ 0 & 1 \end{array}]

dz=κtG

[\begin{array}{l} 1 & 0 \\ 0 & 1 \end{array}]

(10)

κ为与形状相关的剪切系数,κ=5/6;G为剪切模量;矩阵D₀为基础本构系数矩阵,表达式为

D₀=

\frac{E}{1 - ν^{2}} [\begin{array}{l} 1 & ν & 0 \\ ν & 1 & 0 \\ 0 & 0 & (1 - ν) / 2 \end{array}]

(11)

E为弹性模量,ν为泊松比。

2.2 刚柔耦合动力学控制方程

图4为链节i刚柔耦合示意图,其中变形体i通过有限元方法离散。图4中:OX₀Y₀Z₀为惯性坐标系,O_ix_iy_iz_i为连体坐标系,O_ijx_ijy_ijz_ij为变形体i上第j个单元的单元坐标系;c点为j单元上的任意一点,变形后为c'点;r_i为惯性坐标系原点至连体坐标系原点的矢径;r_ic为连体坐标系原点至c'点的矢径;r'_c为惯性坐标系原点至c'点的矢径;ρ_c为连体坐标系到c点的矢径;u_c为变形量,可通过单元形函数与节点位移表示

u_c=NL_ij

q_{f}^{j}

(12)

N为单元形函数,L_ij为单元坐标系相对连体坐标系的方向余弦A_ij组成的对角阵,

q_{f}^{j}

为第j个单元节点的平动变形矢量。

图4 刚柔耦合示意图

Fig.4 Schematic diagram of rigid-flexible coupling

Full size|PPT slide

则惯性坐标系原点至c'点的矢径为

r_c_'=r_i+r_ic=r_i+A_i(ρ_c+u_c)

(13)

式中:A_i为变形体i的连体坐标系相对于惯性坐标系的方向余弦。

对式(12)求时间的1阶和2阶导数,结合虚功率方程可得刚柔耦合控制方程为

ρ \int_{V} v_{c^{'}}^{T} a_{c^{'}} d V + Γ_{G} = 0

(14)

式中:V为变形体体积;v_c'为c'的速度;a_c'为c'的加速度;Γ_G为包含外力、约束力以及变形力引起的惯性力功率。通过对式(14)的变分,可得到刚柔耦合动力学方程为

[\begin{array}{l} ε_{i} \\ a_{i} \\ {\overset{\cdot \cdot}{q}}_{f} \end{array}]

[\begin{array}{l} ω_{i} \\ v_{i} \\ {\overset{\cdot}{q}}_{f} \end{array}]

[\begin{array}{l} θ_{i} \\ u_{i} \\ q_{f} \end{array}]

[\begin{array}{l} Q_{θ} \\ Q_{u} \\ Q_{f} \end{array}]

(15)

式中:M、C分别为等效质量矩阵和等效阻尼矩阵;K为有限元展开时得到的刚度矩阵;ε_i为节点角加速度;a_i为节点加速度;

{\overset{\cdot \cdot}{q}}_{f}

为节点的平动变形加速度;ω_i为节点角速度;v_i为节点速度;

{\overset{\cdot}{q}}_{f}

为节点平动变形速度;θ_i为节点角位移;u_i为节点位移;Q_θ、Q_u和Q_f分别为刚体部分对应的外力矩和外力以及变形体对应的节点力。

2.3 刚-柔约束方程

利用有限元法展开的变形体刚柔耦合控制方程必然包含刚体运动模态,为了获得系统动力学方程的唯一解,需要消除变形体相对连体坐标系的变形运动中包含的刚体运动部分。因此,可取建立连体坐标系的点为参考点,在其上建立刚体运动与变形体运动的位移约束,用以消除变形体运动中包含的刚体运动。

令连体坐标系所在的点为D,假设变形后其坐标变化至D',其各矢径的定义比照点c建立。位移约束建立如下:

\{\begin{array}{l} r_{D'} - r_{D} = 0 \\ θ_{D} = 0 \\ γ_{D} = 0 \end{array}

(16)

式中:r_D为惯性坐标系原点到点D的矢径;r_D'为惯性坐标系原点到点D'的矢径;θ_D为中厚板截面角位移;γ_D为中厚板的截面剪切偏转角位移。

将式(16)对时间求2阶导数,得

A_i

{\overset{\cdot \cdot}{u}}_{D}

-((A_iu_D)×1)ε_i=-2ω_i×(A_i

{\overset{\cdot}{u}}_{D}

)-ω_i×(ω_i×(A_iu_D))

(17)

\{\begin{array}{l} {\overset{\cdot \cdot}{θ}}_{D x} = 0 \\ {\overset{\cdot \cdot}{θ}}_{D y} = 0 \\ \frac{\partial ω_{D}}{\partial x} - {\overset{\cdot \cdot}{θ}}_{D y} = 0 \\ \frac{\partial ω_{D}}{\partial y} - {\overset{\cdot \cdot}{θ}}_{D x} = 0 \end{array}

(18)

式中:u_D、

{\overset{\cdot}{u}}_{D}

、

{\overset{\cdot \cdot}{u}}_{D}

分别为点D的位移、速度、加速度矢量;

{\overset{\cdot \cdot}{θ}}_{D x}

、

{\overset{\cdot \cdot}{θ}}_{D y}

分别为点D的x轴、y轴方向角加速度;ω_D为点D的角速度。

式(18)为中厚板单元截面角位移约束的2阶导形式,若是薄板单元的情况,则去除剪切项约束。

2.4 接触建模

通过2.3节提出的建模方法可以构建以某弹仓为案例的闭式轨道输送链的刚柔耦合动力学模型。链节与链节、链节与滚轮之间的运动学关系通过式(15)建立。滚轮与链轮、滚轮与轨道之间的运动约束则通过接触理论建立^[22-23],接触力模型使用Lankarani-Nikravesh模型描述如式(19)所示,摩擦力使用Coulomb模型描述如式(20)所示。闭式轨道输送链的首尾构件与末位构件之间的运动学关系则通过切断铰的方法建立^[12]。

F_n=Khⁿ+C

\overset{\cdot}{h}

(19)

F_t=-c_fc_dF_n

\frac{v_{t}}{‖ v_{t} ‖}

(20)

式中:F_n为法向碰撞力;K为两个相互接触物体的刚度系数;h为接触体的穿透深度;n为碰撞指数;C为接触碰撞阻尼系数;

\overset{\cdot}{h}

为接触点处的相对碰撞速度;F_t为切向摩擦力;c_f为滑动摩擦系数;c_d为动态修正系数^[24-25];v_t为相对切向速度。

3 系统刚柔耦合方程的建立及实验验证

除了切断铰、刚-柔耦合运动学约束以外,还存在其他运动约束,如速度驱动等。此类额外约束都可以通过第一类拉格朗日方程加载在系统动力学方程中,通用格式^[26]为

\{\begin{array}{l} M \overset{\cdot \cdot}{P} + C \overset{\cdot}{P} + K P + {Φ^{T}}_{P} λ = Q \\ Φ_{P} = 0 \end{array}

(21)

式中:

\overset{\cdot \cdot}{P}

\begin{array}{l} ε & a & {\overset{\cdot \cdot}{q}}_{f} \end{array}

]^T;

\overset{\cdot}{P}

\begin{array}{l} ω & v & {\overset{\cdot}{q}}_{f} \end{array}

]^T;P=[

\begin{array}{l} θ & u & q_{f} \end{array}

]^T;Q=[

\begin{array}{l} Q_{θ} & Q_{u} & Q_{f} \end{array}

]^T;Φ_P为约束方程;λ为拉格朗日乘子。求解式(21),可得到刚柔耦合系统的动态响应。

考虑空载、半载、满载的工况,对刚柔耦合动力学模型进行仿真求解,并与实验台架的结果对比。某弹仓的实验台架如图5所示,弹仓由伺服电机通过减速机驱动,链轮的角位移通过主轴上的齿轮及与角位移传感器的消隙齿轮反馈至外接的角位移传感器。系统模型的输入为减速机末端的输出力矩,直接加载在链轮轴上。输出力矩由伺服电机的电流转化而来,考虑减速机的传动效率。电机的电流可通过电机内部的传感器模块直接获取。

图5 某弹仓实验台架

Fig.5 Experimental device of magazine

Full size|PPT slide

仿真与实验的结果对比如图6所示。

图6 某弹仓仿真和实验结果对比

Fig.6 Comparison of simulated and experimental results of magazine

Full size|PPT slide

设n_t为曲线离散点的数量,y_i为仿真曲线数据点,

_{i}

为实验曲线离散点,

{\bar{y}}_{i}

为实验数据的平均值,基于拟合优度指标计算仿真曲线与实验曲线之间的距离误差,R²=1-

\sqrt{\overset{n_{t}}{\sum_{i = 1}} (y_{i} -_{i})^{2} / \overset{n_{t}}{\sum_{i = 1}} ({\bar{y}}_{i} -_{i})^{2}}

,结果如表2所示,结果越接近1,表明仿真曲线越接近实验结果。由上述对比结果可以看到,弹仓空载、半载和满载工况下,链轮的角位移的变化趋势与实验结果大概一致;且随着负载的增加,链轮角位移的仿真结果愈加接近实验结果。根据图6的输入电机力矩曲线可知,3种工况下,力矩在起始时刻存在突变,因此仿真得到的角速度在起始时刻都有突变,且随着驱动力矩起始值的增大而增大。这是因为建立刚柔耦合动力学模型时,滚轮的中心位置与轮齿啮合圆的圆心位置在轨道中心线上,不与轮齿和轨道接触。比较板单元离散的和实体单元离散的链节模型可知,利用二者建立的刚柔耦合动力学模型得到的结果一致,从而可以采用弹仓刚柔耦合模型开展关键因素影响分析。

表2 不同柔性单元类型计算结果与实验的误差

Table 2 Errors between calculated and experimental results for different types of flexible units

空载、半载与满载	板单元计算结果与实验的误差	实体单元计算结果与实验的误差
空载	0.8925	0.9038
半载	0.9362	0.9393
满载	0.9647	0.9676

4 主要影响因素对弹仓运动影响分析

为了进一步分析弹仓的动力学特性,采用经过实验验证的准确的弹仓刚柔耦合仿真动力学模型探索主要影响因素对弹仓运动的影响。建模的过程中考虑了链节和弹筒的弹性变形、动力系统传动构件的支撑刚度、轨道间隙等影响因素。这些因素影响着轨道链系统的动态特性。除表1的弹仓参数外,弹仓其他基本输入参数如表3所示。

表3 弹仓输入参数

Table 3 Nominal values of magazine input parameters

输入参数	名义值	输入参数	名义值
滚轮半径/mm	15	链轮轴轴承支撑刚度/(N·m^-1)	5×10⁹
链节长度/mm	30	滚轮-轨道间隙/mm	0.3
弹筒-弹丸间隙/mm	0.5	链轮槽半径/mm	15.5
滚轮与链轮的摩擦系数	0.3	弹性模量/MPa	2.1×10⁵
滚轮与轨道的摩擦系数	0.3	泊松比	0.3
上轨道纵向初始位置/mm	0	下轨道纵向初始位置/mm	0
上轨道横向初始位置/mm	0	下轨道横向初始位置/mm	0

4.1 弹性变形的影响

首先,为了验证柔性体对弹仓运动特性的影响,对比分析弹筒、链节柔性化与刚性的仿真计算结果。图7所示为弹筒和链节分别为刚性和柔性时,1号弹筒中的弹丸质心3个方向的加速度对比。由图7可以看出,在运动过程中,刚性体和柔性体下弹丸的加速度状态基本不同,且最大振动时刻存在很大的差异,x轴和y轴方向的刚性振动比柔性振动大,而z轴方向在刚性状态下无振动,柔性体状态下在初始时刻存在较大冲击。由此可见,当弹筒和链节为柔性时,弹仓的运动状态更加接近真实状态,能够提供更加真实的仿真结果,因此对弹筒和链节等关键零部件进行柔性化建模是非常必要的。

图7 弹筒和链节刚性和柔性时弹丸质心加速度对比

Fig.7 Comparison of the accelerations of the mass center of projectile for the rigid and flexible barrels and chains

Full size|PPT slide

4.2 传动构件支撑刚度的影响

支撑刚度是指被支撑构件安装轴承的等效刚度。某种程度上,支撑刚度影响被支撑构件的实际位置,而实际位置的改变也会带来系统动态特性的改变。本文主要考虑动力输出系统的支撑刚度以及驱动链轮安装轴承的等效支撑刚度。不同轴承支撑刚度(N/m)对弹仓运动的影响对比如图8~图12所示,部分结果数据如表4所示。

图8 支撑刚度对弹仓驱动链轮角位移的影响

Fig.8 The influence of support stiffness on the angular displacement of magazine drive sprocket

Full size|PPT slide

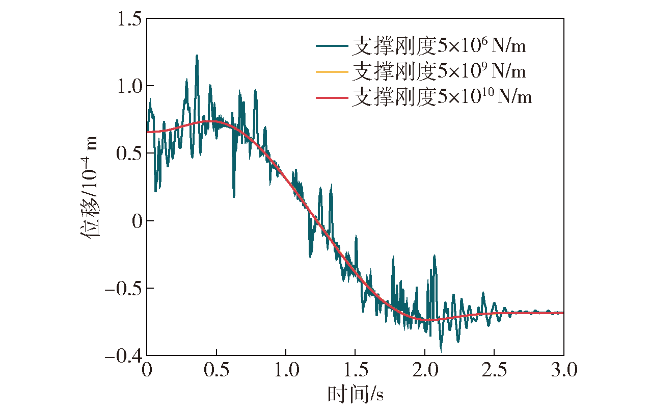
图9 支撑刚度对弹仓驱动链轮横向位移的影响

Fig.9 The influence of support stiffness on the lateral displacement of magazine drive sprocket

Full size|PPT slide

图10 支撑刚度对弹仓驱动链轮横向速度的影响

Fig.10 The influence of support stiffness on the lateral velocity of magazine drive sprocket

Full size|PPT slide

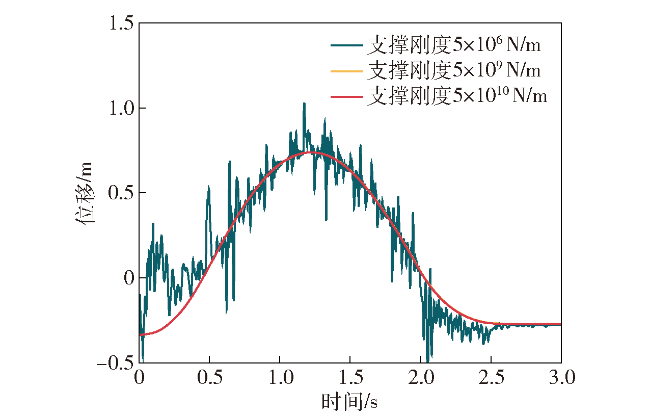
图11 支撑刚度对弹仓驱动链轮纵向位移的影响

Fig.11 The influence of support stiffness on the longitudinal displacement of magazine drive sprocket

Full size|PPT slide

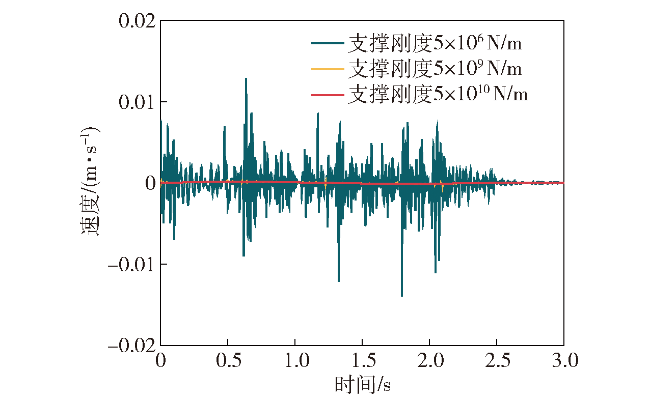
图12 支撑刚度对弹仓驱动链轮纵向速度的影响

Fig.12 The influence of support stiffness on the longitudinal velocity of magazine drive sprocket

Full size|PPT slide

表4 支撑刚度对链轮运动的影响结果

Table 4 The influence of support stiffness on the sprocket motion

刚度/ (N·m^-1)	链轮角位移 (2.5s)/rad	链轮横向位移 (2.07s)/m	链轮横向速度 (2.043s)/(m·s^-1)
5×10⁶	3.9886	-2.64×10^-5	0.0184
5×10⁹	3.9837	-7.33×10^-5	1.87×10^-5
5×10¹⁰	3.9824	-7.34×10^-5	2.7×10^-6

由图8~图12以及表4可以看出,轴承支撑刚度对于链轮横向位移/速度和纵向位移/速度的影响趋势比较类似,当轴承支撑刚度较小时(5×10⁶N/m),链轮的运动会产生较大的振动,稳定性很差;当轴承支撑刚度增加到5×10⁹N/m时,链轮的横向和纵向运动则变得稳定,继续增大轴承的支撑刚度,基本不会影响链轮的运动。

4.3 轨道间隙的影响

轨道间隙c是指滚轮与滚轮轨道之间的间隙,是影响轨道链动态特性的主要因素。轨道间隙对弹仓系统动态特性的影响如图13~图17所示,数值对比如表5所示。

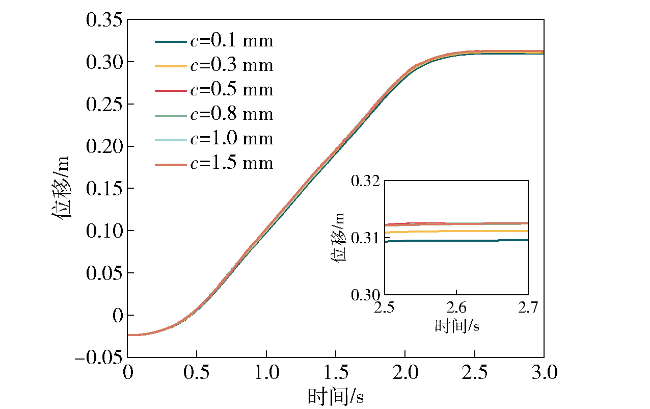
图13 轨道间隙对弹筒1位移的影响

Fig.13 The influence of rail clearance on the displacement of magazine barrel 1

Full size|PPT slide

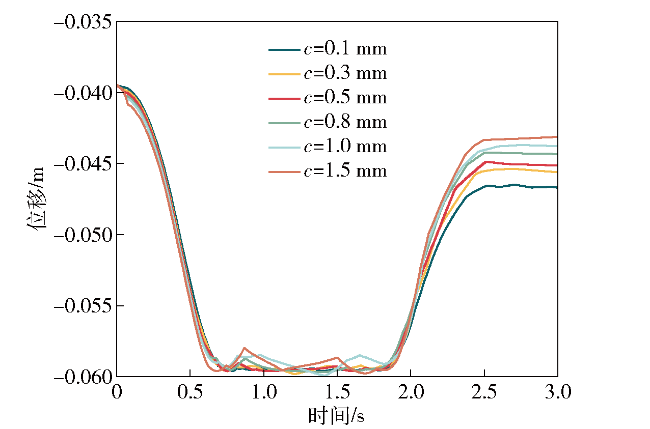
图14 轨道间隙对弹筒1横向位移的影响

Fig.14 The influence of rail clearance on the lateral displacement of magazine barrel 1

Full size|PPT slide

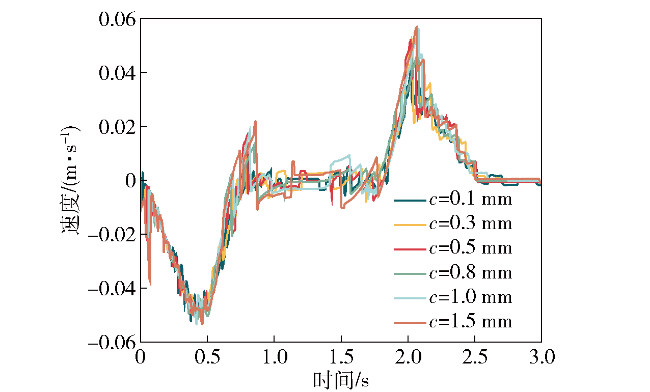
图15 轨道间隙对弹筒1横向速度的影响

Fig.15 The influence of railclearance on the lateral velocity of magazine barrel 1

Full size|PPT slide

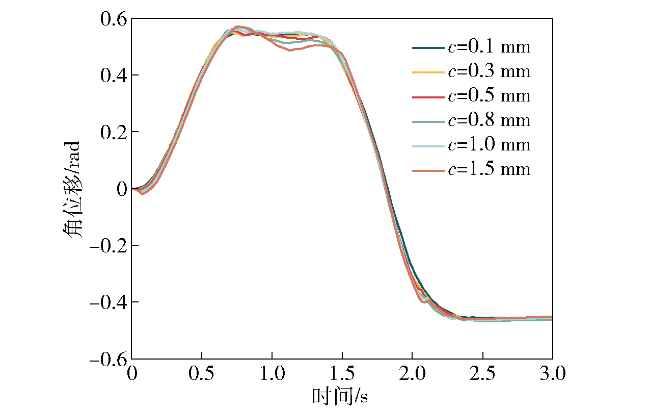
图16 轨道间隙对弹筒1转动角位移的影响

Fig.16 The influence of rail clearance on the angular displacement of magazine barrel 1

Full size|PPT slide

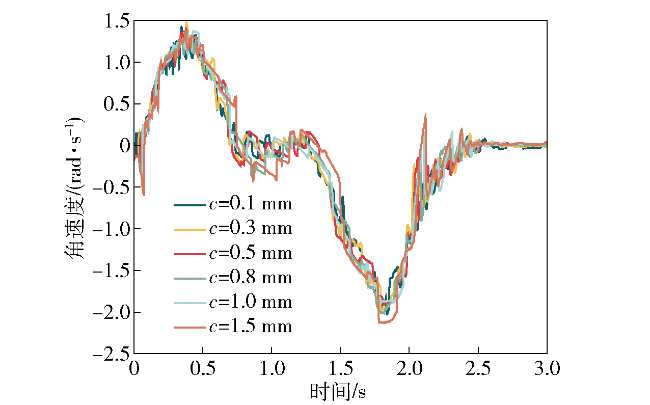
图17 轨道间隙对弹筒1转动角速度的影响

Fig.17 The influence of rail clearance on the angular velocity of magazine barrel 1

Full size|PPT slide

表5 轨道间隙对弹筒运动的影响结果

Table 5 The influence of rail clearance on the magazine barrel motion

间隙/ mm	弹筒1 位移 (3.0s)/ m	弹筒1 横向位移 (3.0s)/ m	弹筒1 横向速度 (2.0s)/ m	弹筒1转动角位移 (3.0s)/ m	弹筒1转动角速度 (3.0s)/ m
0.1	0.3029	-0.04672	0.03141	-0.40068	0.02719
0.3	0.3109	-0.04563	0.04223	-0.46204	-0.02007
0.5	0.3123	-0.04515	0.04711	-0.45678	0.01377
0.8	0.3124	-0.04435	0.03350	-0.46381	-0.00474
1.0	0.3125	-0.04379	0.03930	-0.45623	0.01454
1.5	0.3126	-0.04316	0.04355	-0.45127	0.02767

由图13和表5可知,当间隙增大至0.5mm以后,1号弹筒到位时的位置不再明显变化,这是闭式轨道链系统的独有特性。当链轮运动时,链条在链轮的作用下有离心的趋势;当链节首尾相接形成闭环时,对链条向外运动的趋势进行了约束。若轨道间隙较小,则当链条向外运动时,先受到轨道外侧的约束;当轨道间隙足够大时,链条会优先受到闭环结构的运动约束,此现象可从图14和表5中看出。图14中,当轨道间隙较小时,1号弹筒内外偏离的位移基本一致;当轨道间隙较大时,1号弹筒向内侧偏离的位移明显大于向外侧偏离的位移,且随着间隙的增大,向内侧偏离的位移增大,而向外侧偏离的位移则不一定随着间隙的增大而增大。此外,随着轨道间隙的增大会带来较大的横向振动。由图14~图17可知,随着间隙的增大,弹筒的横向位移、横向速度、转动角位移、转动角速度也会随之增大。而且,较大的间隙也会带来较大的速度波动。

4.4 轨道错位的影响

相对于单层轨道输送链系统,双层轨道链对装配误差的要求更高。当双层轨道发生错位时,链传动的动态特性会发生变化。本文只讨论轨道错位对系统动态特性的定性影响,用以筛选双层轨道装配误差项中对系统特性影响比较大的因素。本节轨道相对位置和姿态的变化幅度取决于滚轮和轨道之间的理论间隙值,以理论间隙值的10%误差作为轨道错位的输入。轨道错位对系统动态特性的影响如图18所示,到位角位移数值如表6所示。

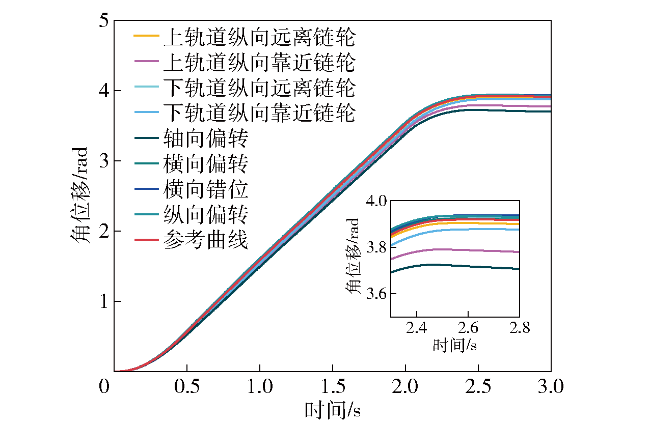
图18 轨道错位对链轮角位移的影响

Fig.18 The effect of rail misalignment on the angular displacement of sprocket

Full size|PPT slide

表6 轨道错位对链轮角位移到位的数值结果

Table 6 The effect ofrail misalignment on the angular displacement in place of the sprocket

影响因素	到位角位移/rad
参考值	3.91195
上轨道纵向远离链轮	3.89348
上轨道纵向靠近链轮	3.77134
下轨道纵向远离链轮	3.92077
下轨道纵向靠近链轮	3.87183
轴向偏转	3.69871
横向偏转	3.91233
横向错位	3.9314
纵向偏转	3.9236

由图18和表6可知:轨道发生轴向偏转和纵向偏移靠近链轮错位时,链轮角位移受到的影响最大;横向偏移错位时,几乎不受影响。这是因为当轨道发生纵向偏移错位时,圆弧轨道和轮齿之间的空间被压缩,影响到滚轮在主动链轮处圆弧轨道中的运动特性。因此,在装配双层轨道输送链时,需要注意滚轮的运动空间,进一步地,需要注意两层轨道的纵向相对位置。

5 结论

本文提出一种针对装填系统轨道输送链的刚柔耦合动力学建模方法。该方法运用相对坐标法建立链节与链节、链节与滚轮之间的运动学约束关系,运用Reissner-Mindlin中厚板单元描述链节的弹性变形运动,运用接触碰撞理论描述链轮与滚轮、轨道与滚轮之间的接触关系,用Lankarani-Nikravesh模型描述由此产生的接触力,用Coulomb摩擦模型描述接触面之间的摩擦力。随后依据装填系统的结构特点,分别基于Reissner-Mindlin中厚板单元描述链节的弹性变形运动,建立了以某弹仓为案例的闭式轨道输送链系统的动力学模型,并将所得仿真结果与实验数据进行对比。模型建立过程中,除了链节的弹性变形运动、输送轨道间的运动间隙等因素之外,还考虑了动力系统传动构件的支撑刚度和轨道错位的影响,且针对这些因素的变化分析了系统的动态影响。得出主要结论如下:

1)基于链节弹性变形运动两种描述方式建立的刚柔耦合动力学模型求得的结果高度一致。仿真结果与实验结果也基本一致,且随着负载的增加,仿真结果也越趋近于实验结果。

2)传动构件的支撑刚度对系统动态响应的影响取决于动力系统的结构特性。链轮轴承的支撑刚度较小时,链轮运动会有较大的抖动,当增大到一定程度时(5×10⁹N/m),链轮运动变得平稳,且不再随轴承支撑刚度的变大而变化。

3)随着轨道间隙的增大,弹仓的驱动链轮的角速度先增大再基本保持一致。但是随着轨道间隙的增大,其链传动构件的横向振动都会增大,而横向振动的增大则会带来运动的不平稳性。

4)上下轨道的错位会对弹仓链传动的运动特性有较大影响,在加工装配时要保证上下轨道的一致性。

此外,本文所提方法可以推广至装填系统的其他含有链传动的子系统(例如输弹机、输药机、药仓等)仿真建模中,以节约计算成本,获得实验难以采集的故障数据。未来还可开展装填系统的精准故障诊断和可靠性提升,例如:1)开展链条松弛、跳齿、链轮磨损等细致故障的模拟,进而通过仿真分析结果识别出装填系统中常见故障的特征;2)开展高速、重载、恶劣环境等复杂工况下的故障识别,进而为用户识别出难以检测的早期故障;3)通过装填系统仿真模型分析链条和链轮的应力分布、动态载荷,预测材料疲劳寿命,帮助确定装填系统的薄弱环节,从而在设计阶段进行优化,延长装填系统的使用寿命,提升其可靠性;4)将装填系统刚柔耦合仿真模型与实时监控系统结合,通过分析实际操作数据与仿真模型的差异,预测潜在的故障,制定维护计划,从而降低装填系统故障率;基于仿真结果,动态调整维护周期,避免过度维护或维护不足,提高装填系统的可靠性。

参考文献

原文顺序 | 文献年度倒序 | 文中引用次数倒序

[1]	钱林方, 徐亚栋, 陈龙淼. 车载炮射击理论和方法[M]. 北京: 科学出版社, 2022. QIAN L F, XU Y D, CHEN L M. Shooting theory and methods of vehicle mounted cannon[M]. Beijing: Science Press, 2022. (in Chinese) 本文引用 [1]

[2]	侯保林, 樵军谋, 刘琮敏. 火炮自动装填[M]. 北京: 兵器工业出版社, 2010. HOU B L, QIAO J M, LIU C M. Automatic loader of artillery[M]. Beijing: Publishing House of Ordnance Industry, 2010. (in Chinese) 本文引用 [1]

[3]

赵伟, 侯保林, 闫少军, 等. 链式回转弹仓区间不确定性动力学模型[J]. 兵工学报, 2024, 45(6): 1991-2002.

https://doi.org/10.12382/bgxb.2023.0379

摘要

针对具有区间不确定性参数的辨识问题,提出一种基于区间可能度转换模型的区间不确定性参数的双层嵌套辨识(Double-layer Nested Identification,DNI)方法。通过将待辨识参数分为两类,利用DNI方法辨识出第1类确定性参数,再通过基于DNI思想的区间优化方法优化第2类区间不确定性参数的区间范围;面向嵌套策略类型方法计算量庞大且效率低的问题,选用贝叶斯优化-粒子群优化(Bayesian Optimization-Particle Swarm Optimization,BO-PSO)方法作为内层算法以提高求解效率。DNI方法的内层利用BO-PSO方法计算区间上下界,外层利用改进型布谷鸟搜索(Improved Cuckoo Search,ICS)方法辨识特定参数。为进一步缩短求解时间,提出一种ICS多核极限学习机(ICS-Multiple Kernel-Extreme Learning Machine,ICS-MK-ELM)代理模型,ICS-MK-ELM代理模型克服了人工调节每个核函数超参数的困难,并且模型预测精度明显高于核ELM(Kernel ELM,KELM)和MK-ELM;将DNI方法应用于链式回转弹仓的参数辨识,解决了链式弹仓具有区间不确定性参数的辨识困难的问题,参数辨识结果表明所提DNI方法以及基于DNI思想的区间优化方法具有更高的精度和稳定性。

ZHAO

, HOU

B L

, YAN

S J

, et al. A dynamic model of interval uncertainty of rotational chain shell magazine[J]. Acta Armamentarii, 2024, 45(6):1991-2002. (in Chinese)

https://doi.org/10.12382/bgxb.2023.0379

本文引用 [1] 摘要

For the identification problem with interval uncertain parameters, a double-layer nested identification (DNI) method based on an interval possibility degree transformation model is proposed. By dividing the parameters to be identified into two categories, the first type of deterministic parameters are identified by DNI method, and the interval range of the second type of interval uncertainty parameters is optimized by the DNI-based interval optimization method. The BO-PSO algorithm is chosen as the inner-layer algorithm to improve the efficiency of the nested strategy type method. For the inner layer of DNI method, BO-PSO method is used to calculate the upper and lower bounds of interval, and for the outer layer, ICS method is used to identify the specific parameters. In order to shorten the solving time, an ICS-MK-ELM agent model is proposed. The ICS-MK-ELM agent model overcomes the difficulty of manually adjusting the hyper-parameters of each kernel function, and the prediction precision of the model is obviously higher than those of KELM and MK-ELM. Finally, the DNI method is applied to the parameter identification of the rotational chain shell magazine, which solves the problem of the parameter identification of the chain-type magazine with interval uncertainty. The results of parameter identification show that the DNI method and the interval optimization method based on DNI have higher accuracy and stability.

[4]

文浩, 侯保林, 林瑜斌, 等. 曲线链式回转弹仓动力学模型不确定参数辨识[J]. 兵工学报, 2024, 45(5): 1460-1471.

https://doi.org/10.12382/bgxb.2022.1196

摘要

为了准确模拟曲线链式回转弹仓输送弹药过程中的非线性动力学特性,根据系统的拓扑结构和控制原理建立包含不确定参数的动力学模型。利用优化设计思想,基于系统测试数据建立不确定参数辨识模型。提出一种函数型时间序列相似度作为辨识准则,采用基于径向基函数的高维模型表示和径向基函数分别构建从机械系统和控制系统不确定参数到辨识准则的代理模型。将麻雀搜索算法嵌入岛屿模型进行多种群结构化,形成岛屿麻雀搜索算法,进行寻优求解。以工况1测试数据为基准,对机械系统和控制系统的不确定参数进行辨识。研究结果表明,辨识后的动力学模型对两种工况的输出结果与测试数据相似度较高,验证了建模的准确性和辨识的有效性,为动作可靠性分析和故障诊断研究提供了可靠的样本数据来源。

WEN

, HOU

B L

, LIN

Y B

, et al. Dynamic model uncertain parameter identification for a curved chain rotary shell magazine[J]. Acta Armamentarii, 2024, 45(5): 1460-1471. (in Chinese)

https://doi.org/10.12382/bgxb.2022.1196

本文引用 [1] 摘要

To accurately simulate the nonlinear dynamics of a curved chain rotary shell magazine during the delivery of ammunition, a dynamic model containing uncertain parameters is established according to the system topology and control principle. An uncertain parameter identification model for the dynamic model is developed based on the system test data using the optimization design idea. A functional time series similarity is proposed as the identification criterion. The high-dimensional model representation based on the radial basis function and the radial basis function are used to construct the surrogate models from the uncertain parameters of the mechanical and control systems to the identification criterion, respectively. The sparrow search algorithm is embedded into an island model for multi-population structuring to form an island sparrow search algorithm for optimization. The uncertain parameters of the mechanical and control systems are identified successively by taking the test data of working condition 1 as the benchmark. The results show that the outputs of the identified dynamic model for the two operating conditions are similar to the test data, which verifies the accuracy of modelling and the validity of identification, and provides a reliable sample data source for action reliability analysis and fault diagnosis research.

[5]

马超超, 许金, 贾正荣, 等. 计及配合间隙的电磁发射重载链传动机构优化设计方法[J/OL]. 海军工程大学学报: 1-7 [2024-01-07]. http://kns.cnki.net/kcms/detail/42.1106.E.20231107.1417.010.html.

http://kns.cnki.net/kcms/detail/42.1106.E.20231107.1417.010.html

C C

, XU

, JIA

Z R

, et al. Optimization design method of heavy-duty chain transmission mechanism used for electromagnetic launch considering fit clearance[J/OL]. Journal of Naval University of Engineering, 1-7 [2024-01-07]. (in Chinese)

本文引用 [1]

[6]

陈冬, 钱林方, 陈志群, 等. 基于改进拟连续算法的回转弹仓位置控制[J]. 兵工学报, 2024, 45(5): 1436-1448.

https://doi.org/10.12382/bgxb.2023.0064

摘要

为提高大口径火炮自动装填过程中回转弹仓工作的精确性和鲁棒性,在分析现有拟连续算法相关研究内容的基础上,设计一种全新的改进拟连续控制器对回转弹仓进行位置控制。通过与滑模扰动观测器相结合,新控制器增益不依赖于系统扰动的不确定性边界,且不需引入额外的控制器参数,降低了控制器的设计和调试难度。通过Lyapunov方程验证控制器本身及闭环系统的稳定性。仿真和试验结果表明:新设计的控制器相对于已有拟连续算法具有优越性,在受到不确定时变负载和不确定参数扰动的情况下,新设计的改进控制器在应用于回转弹仓时,在趋近段可以获得更快的收敛速度,减小到位超调量,并在滑动段有效减弱抖振。

CHEN

, QIAN

L F

, CHEN

Z Q

, et al. An improved quasi-continuous algorithm for rotational shell magazine position control[J]. Acta Armamentarii, 2024, 45(5): 1436-1448. (in Chinese)

https://doi.org/10.12382/bgxb.2023.0064

本文引用 [1] 摘要

Based on the existing researches on quasi-continuous algorithm, a novel improved quasi-continuous controller is designed to improve the precision and robustness of rotational shell magazine position control in the automatic loading process of a large caliber artillery.By combining a sliding mode disturbance observer, the novel controller is independent of the unknown system uncertainty boundary, and no new parameters are introduced, which will lower the difficulties of controller designing and adjusting.The stabilities of controller and close-loop scheme are verified by Lyapunov functions. The simulated and experimental results have demonstrated the superiority of the improved controller over the existing quasi-continuous algorithm.In the presence of unknown time-varying disturbance and uncertain parameters, the improved controller could achieve a higher convergence rate in reaching phase, reduce the overshoot and restrain chattering in sliding phase while performed on the magazine.

[7]

鲍丹, 卫俞凯, 金鑫, 等. 考虑输出约束和输入饱和的弹仓自适应控制[J]. 兵工学报, 2024, 45(3): 789-797.

https://doi.org/10.12382/bgxb.2022.0896

摘要

针对存在参数不确定性和外部扰动的某链式回转弹仓的位置跟踪控制问题,提出一种自适应控制方案。该方案基于神经模糊系统(Neuro-Fuzzy System, NFS)、非线性扰动观测器(Nonlinear Disturbance Observer, NDO)及障碍Lyapunov函数(Barrier Lyapunov Function, BLF),在实现高精度控制的同时满足输出约束和输入饱和的工程条件。通过BLF的设计,保证弹仓的位移跟踪误差约束在给定范围内。结合神经网络的函数逼近能力和模糊逻辑系统的推理能力,用于估计系统中的不确定性,减小对模型的依赖;两者结合的NFS作为NDO的一部分,进一步补偿估计误差和外部扰动,提高控制性能。此外,控制器设计考虑了运动过程中的执行器输入饱和问题。仿真结果表明,所设计的控制器在3种典型工况以及系统参数变化情况下均可实现弹仓的高精度位置跟踪控制,满足系统的约束条件。

BAO

, WEI

Y K

, JIN

, et al. Adaptive control of magazines considering output constraints and input saturation[J]. Acta Armamentarii, 2024, 45(3): 789-797. (in Chinese)

https://doi.org/10.12382/bgxb.2022.0896

本文引用 [1] 摘要

An adaptive control scheme is proposed for the position tracking control of a chain rotary magazine with parameter uncertainties and external disturbances. Based on neuro-fuzzy system ( NFS), nonlinear disturbance observer (NDO), and barrier Lyapunov function (BLF), the proposed scheme achieves high precision control while satisfying the engineering conditions of output constraint and input saturation. The BLF design ensures that the position tracking error of magazine is constrained within a bounded range. The function approximation ability of neural network and the reasoning ability of fuzzy logic system are combined to estimate the uncertainties of the system and reduce the dependence on the model. The combined NFS is used as part of NDO to further compensate for estimation errors and external disturbances and improve the control performance. In addition, the actuator input saturation problem is considered in the design of the controller. The simulated results show that the designed controller can realize the high-precision position tracking control of the magazine under three typical working conditions and system parameter changes, and meet the constraints of the system.

[8]	郝驰宇, 冯广斌, 闫鹏程, 等. 基于MFBD的输弹机刚柔耦合动力学建模及仿真分析[J]. 振动与冲击, 2016, 35(15):161-167. HAO C Y, FENG G B, YAN P C, et al. Rigid-flexible coupled dynamic modeling and simulation for a ramming mechanism based on MFBD[J]. Journal of Vibration and Shock, 2016, 35(15):161-167. (in Chinese) 本文引用 [1]

[9]	闫鹏程, 郝驰宇, 孙华刚, 等. 基于RecurDyn的开式链传动输弹机动力学联合仿真研究[J]. 火炮发射与控制学报, 2015, 36(2):31-35. YAN P C, HAO C Y, SUN H G, et al. Study on dynamical cosimulation of open chain Drive ramming mechanism based on recurDyn[J]. Journal of Gun Launch & Control, 2015, 36(2):31-35. (in Chinese) 本文引用 [1]

[10]	陆栋栋. 重型单向齿形推弹链的设计研究[D]. 南京: 南京理工大学, 2016. LU D D. Study on the design of heavy single tooth push-pull chain[D]. Nanjing: Nanjing University of Science and Technology, 2016. (in Chinese) 本文引用 [1]

[11]

李伟, 马吉胜, 狄长春, 等. 考虑参数随机性的供输弹系统动力学及动作可靠性仿真研究[J]. 兵工学报, 2012, 33(6):747-752.

摘要

利用MSC.Adams和Easy5仿真软件建立了供输弹系统机电液耦合的动力学模型，通过VV&A证明了仿真模型的可信度。针对MCS求解复杂结构系统随机动力学问题时计算量过于庞大的难点，提出了虚拟样机—蒙特卡洛模拟法—支持向量机（VP-MCS-SVM）动力学随机响应求解方法，高效地完成了供输弹系统随机动力学的仿真求解。结合统计推断理论和可靠性分析理论探讨了供输弹系统动作可靠性及随机参数分布特征漂移时的动作可靠性问题利用MSC.Adams和Easy5仿真软件建立了供输弹系统机电液耦合的动力学模型，通过VV&A证明了仿真模型的可信度。针对MCS求解复杂结构系统随机动力学问题时计算量过于庞大的难点，提出了虚拟样机—蒙特卡洛模拟法—支持向量机（VP-MCS-SVM）动力学随机响应求解方法，高效地完成了供输弹系统随机动力学的仿真求解。结合统计推断理论和可靠性分析理论探讨了供输弹系统动作可靠性及随机参数分布特征漂移时的动作可靠性问题为复杂系统动作可靠性的评估提供了新的思路。

, MA

J S

, DI

C C

, et al. Simulation research on dynamics of ramming system and action reliability considering the randomness of the parameters[J]. Acta Armamentarii, 2012, 33(6): 747-752. (in Chinese)

本文引用 [1]

[12]	LI Y, QIAN L F, CHEN G S, et al. Multiple clearance robustness optimization of a chain ramming machine based on a data-driven model[J]. Nonlinear Dynamics, 2023, 111(15): 13807-13828. 本文引用 [2]

[13]	WEI K, CHEN L M, ZOU Q. Model-driven full system dynamics estimation of PMSM-driven chain shell magazine[J]. Defence Technology, 2024, 39:147-156. 本文引用 [1]

[14]

张雷雨, 李剑锋, 杨洋. 装甲车辆用立式弹药舱的设计与动力学分析[J]. 兵工学报 2017, 38(5): 843-851.

https://doi.org/10.3969/j.issn.1000-1093.2017.05.002

摘要

为分析输送链条的动力学特性和弹药的稳定性，将所有链节及弹架两侧双排滚子简化为弹簧阻尼单元，采用多体系统动力学和运动弹性动力学理论，建立输送链条的完整动力学模型和弹药的稳定性模型。借助Matlab软件，对输送链条的整体动力学模型进行数值仿真，并求解弹药的稳定性模型。通过数值仿真结果可知：在不同驱动功率下输送链条的速度、加速度均窄幅波动；轨迹线的形状特征决定了弹药离心力的动力学响应和突变特性，离心力的突变特性对弹药运动法线方向稳定性具有较大的影响，而弹药在运动切线方向上的稳定性主要受自身惯性和输送链条的动力学参数影响。根据弹药上部的摆动位移响应可知，弹药在运动法线方向和切线方向具有较好的动态稳定性。采用试验测量方法，得到输送链条的切线方向加速度与弹架的法线方向加速度值，测量数据与仿真结果较为吻合。

ZHANG

L Y

, LI

J F

, YANG

. Design and dynamics analysis of vertical ammunition cabin for armored vehicle[J]. Acta Armamentarii, 2017, 38(5): 843-851. (in Chinese)

本文引用 [1]

[15]

王光建, 姜铁牛. 弹链系统间隙铰多体动力学模型仿真与试验[J]. 机械工程学报, 2008, 44(5): 238-241.

摘要

传统的弹链系统力学模型，常常简化为平面内的运动，此模型对于分析弹链系统的横向运动、窜弹等问题有局限性。研究具有螺旋导引的弹链系统纵向和横向运动规律；建立含间隙铰碰撞的多体动力学模型；用等效弹簧阻尼模型对弹链系统的碰撞和接触进行模拟；对上述模型进行仿真和试验，结果表明：该力学模型能够较真实反映系统的运动规律，能对弹链系统的运动进行很好的预测和分析。

WANG

G J

, JIANG

T N

. Simulation and experiment of multi-body system dynamic model with clearance joint for ammunition belt system[J]. Chinese Journal of Mechanical Engineering, 2008, 44(5):238-241. (in Chinese)

本文引用 [1]

[16]

刘太素, 钱林方, 陈光宋, 等. 某输弹机开式链传动建模及动力学特性分析[J]. 兵工学报, 2018, 39(11): 2109-2117.

https://doi.org/10.3969/j.issn.1000-1093.2018.11.004

摘要

为分析某输弹机开式链传动机构在工作过程中的运动学精度和动力学特性，描述了滚轮与链轮齿槽之间的几何关系和接触模式以及链节之间的接触。针对不同的接触位置和接触模式分别建立了法向接触力模型和平面接触力模型，建立了某输弹机开式链传动机构多刚体动力学模型。分析了不同滚轮与链轮齿槽之间的接触特性，讨论了滚轮与链轮齿槽之间间隙变化对系统运动学精度及动力学特性的影响。研究结果表明：滚轮与链轮齿槽之间间隙的存在及大小变化对某输弹机开式链传动机构动力学特性具有很大影响，在工程实际中需要合理控制间隙。

LIU

T S

, QIAN

L F

, CHEN

G S

, et al. Dynamics modeling and analysis of open chain drive transmission for a ramming mechanism[J]. Acta Armamentarii, 2018, 39(11): 2109-2117. (in Chinese)

本文引用 [1]

[17]	魏继卿, 许耀峰, 刘小蒙, 等. 自动弹仓回转选弹动力学仿真及优化[J]. 火炮发射与控制学报 2015, 36(2): 36-39. WEI J Q, XU Y F, LIU X M, et al. Dynamics simulation and optimization of automatic magazine’s turning-round shell-selecting device[J]. Journal of Gun Launch & Control, 2015, 36(2): 36-39. (in Chinese) 本文引用 [1]

[18]

胡胜海, 郭彬, 邓坤秀, 等. 含非线性接触碰撞的大口径舰炮弹链柔性铰多体模型[J]. 哈尔滨工程大学学报, 2011, 32(9): 1217-1222.

S H

, GUO

, DENG

K X

, et al. A multibody model with flexible joints and the nonlinear contact-impact of an ammunition chain of a large caliber naval gun[J]. Journal of Harbin Engineering University, 2011, 32(9): 1217-1222. (in Chinese)

本文引用 [1]

[19]	CHEN G S, CHEN L M, TANG J S. An edge center based strain-smoothing element with discrete shear gap for the analysis of Reissner-Mindlin shell[J]. Thin-Walled Structures, 2022, 175: 109140. 本文引用 [2]

[20]	TANG J S, QIAN L F, CHEN L M, et al. Flexible multibody dynamic analysis of shells with an edge center-based strain smoothing MITC method[J]. Nonlinear Dynamics, 2023, 111: 3253-3277. 本文引用 [2]

[21]	TANG J S, QIAN L F, MA J, et al. Knowledge-dominated and data-driven rigid-flexible coupling dynamics for rotating flexible structure[J]. Knowledge-Based Systems, 2024, 296: 111853. 本文引用 [2]

[22]	MA J, CHEN G S, JI L, et al. A general methodology to establish the contact force model for complex contacting surfaces[J]. Mechanical Systems and Signal Processing, 2020, 140: 106678. 本文引用 [1]

[23]	LIU T S, NIU Y Y, CHEN G S. A general methodology for simulation model validation and model updating of the coordination mechanism with uncertainty[J]. Journal of Mechanical Science and Technology, 2023, 37(12): 6271-6286. 本文引用 [1]

[24]	FLORES P. Dynamic analysis of mechanical systems with imperfect kinematic joints[D]. Braga, Portugal: University of Minho, 2004. 本文引用 [1]

[25]	MA J, WANG J, PENG J, et al. Data-driven modeling for complex contacting phenomena via improved neural networks considering link switches[J]. Mechanism and Machine Theory, 2024, 191:105521. 本文引用 [1]

[26]	陈光宋. 弹炮耦合系统动力学及关键参数识别研究[D]. 南京: 南京理工大学, 2016. CHEN G S. The study on the dynamic of the projectile-barrel coupled system and the corresponding key parameters[D]. Nanjing: Nanjing University of Science and Technology, 2016. (in Chinese) 本文引用 [1]

PDF(8140 KB)

Accesses

Citation

Detail

段落导航

摘要
Abstract
关键词
Key words
引用本文
基金
0 引言
1 某链式回转弹仓模型描述
图1 弹仓结构组成
图2 弹仓主要结构拓扑关系
表1 构件的质量、惯量参数
2 基于中厚板结构的链节力学模型
2.1 Reissner-Mindlin中厚板建模
图3 变形挠度和转角的方向
2.2 刚柔耦合动力学控制方程
图4 刚柔耦合示意图
2.3 刚-柔约束方程
2.4 接触建模
3 系统刚柔耦合方程的建立及实验验证
图5 某弹仓实验台架
图6 某弹仓仿真和实验结果对比
表2 不同柔性单元类型计算结果与实验的误差
4 主要影响因素对弹仓运动影响分析
表3 弹仓输入参数
4.1 弹性变形的影响
图7 弹筒和链节刚性和柔性时弹丸质心加速度对比
4.2 传动构件支撑刚度的影响
图8 支撑刚度对弹仓驱动链轮角位移的影响
图9 支撑刚度对弹仓驱动链轮横向位移的影响
图10 支撑刚度对弹仓驱动链轮横向速度的影响
图11 支撑刚度对弹仓驱动链轮纵向位移的影响
图12 支撑刚度对弹仓驱动链轮纵向速度的影响
表4 支撑刚度对链轮运动的影响结果
4.3 轨道间隙的影响
图13 轨道间隙对弹筒1位移的影响
图14 轨道间隙对弹筒1横向位移的影响
图15 轨道间隙对弹筒1横向速度的影响
图16 轨道间隙对弹筒1转动角位移的影响
图17 轨道间隙对弹筒1转动角速度的影响
表5 轨道间隙对弹筒运动的影响结果
4.4 轨道错位的影响
图18 轨道错位对链轮角位移的影响
表6 轨道错位对链轮角位移到位的数值结果
5 结论
参考文献

收稿日期	修回日期	出版日期
2024-08-14	2024-10-12	2024-11-30
录用日期	发布日期
2024-10-13	2024-11-26

模态框（Modal）标题

选择文件类型/文献管理软件名称

选择包含的内容

摘要

Abstract

关键词

Key words

引用本文

基金

0 引言

1 某链式回转弹仓模型描述

图1 弹仓结构组成

图2 弹仓主要结构拓扑关系

表1 构件的质量、惯量参数

2 基于中厚板结构的链节力学模型

2.1 Reissner-Mindlin中厚板建模

图3 变形挠度和转角的方向

2.2 刚柔耦合动力学控制方程

图4 刚柔耦合示意图

2.3 刚-柔约束方程

2.4 接触建模

3 系统刚柔耦合方程的建立及实验验证

图5 某弹仓实验台架

图6 某弹仓仿真和实验结果对比

表2 不同柔性单元类型计算结果与实验的误差

4 主要影响因素对弹仓运动影响分析

表3 弹仓输入参数

4.1 弹性变形的影响

图7 弹筒和链节刚性和柔性时弹丸质心加速度对比

4.2 传动构件支撑刚度的影响

图8 支撑刚度对弹仓驱动链轮角位移的影响

图9 支撑刚度对弹仓驱动链轮横向位移的影响

图10 支撑刚度对弹仓驱动链轮横向速度的影响

图11 支撑刚度对弹仓驱动链轮纵向位移的影响

图12 支撑刚度对弹仓驱动链轮纵向速度的影响

表4 支撑刚度对链轮运动的影响结果

4.3 轨道间隙的影响

图13 轨道间隙对弹筒1位移的影响

图14 轨道间隙对弹筒1横向位移的影响

图15 轨道间隙对弹筒1横向速度的影响

图16 轨道间隙对弹筒1转动角位移的影响

图17 轨道间隙对弹筒1转动角速度的影响

表5 轨道间隙对弹筒运动的影响结果

4.4 轨道错位的影响

图18 轨道错位对链轮角位移的影响

表6 轨道错位对链轮角位移到位的数值结果

5 结论

{{custom_sec.title}}

{{custom_sec.title}}

参考文献

{{custom_fnGroup.title_cn}}

脚注