变截面弹体斜侵彻两层间隔钢靶弹道特性

蒋腾; 武海军; 邓希旻; 全鑫; 董恒; 黄风雷

doi:10.12382/bgxb.2024.0019

PDF(23699 KB)

兵工学报 ›› 2025, Vol. 46 ›› Issue (2) : 240019. DOI: 10.12382/bgxb.2024.0019

变截面弹体斜侵彻两层间隔钢靶弹道特性

作者信息 +

Study on Ballistic Characteristics of Variable Cross-section Projectile Obliquely Penetrating Two-layer Spacer Steel Target

Author information +

本文二维码

文章历史 +

摘要

为研究变截面弹体斜侵彻两层间隔钢靶时结构特征对弹道特性的影响规律,开展椭圆等截面、椭圆变截面弹体在1020m/s初速、5°着角条件下斜侵彻两层间隔钢靶实验,结合数值模拟对比圆等截面、椭圆等截面、圆变截面和椭圆变截面弹体在斜侵彻钢靶过程中的弹道轨迹、速度、偏转角、纵向位移和纵向加速度的变化情况,揭示变截面弹体结构特征影响弹道稳定性的物理机制。研究结果表明:当弹体初始撞击速度较大、弹肩处横截面面积一致及变截面角度在0°~2.5°范围内时,不同横截面形状和变截面角度弹体在斜侵彻两层间隔钢靶过程中的速度变化差异很小;对于变截面弹体,可以通过改变变截面结构特征找到一个使得弹体贯穿首层靶板后纵向位移基本为零的临界变截面角度;不同横截面形状的变截面弹体受变截面角度对贯穿钢靶后纵向运动、姿态偏转的敏感程度不同,横截面形状的长短轴之比越大,变截面角度对偏转角速度的影响越大;变截面角度会影响弹体穿靶过程中的受力方向,可能导致弹体受力出现反转现象。相关研究对变截面弹体结构特征参数的优化、变截面弹体斜侵彻两层间隔钢靶弹道特性预测具有较好的指导价值。

Abstract

The influence of the structural characteristics of variable cross-section projectile on the ballistic characteristics during obliquely penetrating the two-layer spaced steel targets is studied.The elliptical and variable cross-section projectiles obliquely penetrate a two-layer spaced steel target at an initial velocity of 1020m/s and an impact angle of 5° in the experiments.The trajectories,velocities,deflection angles,longitudinal displacements and longitudinal accelerations of circular and elliptical equal cross-section projectiles,and circular-and elliptical-variable cross-section projectiles during obliquely penetrating the steel target are compared by numerical simulations,and the physical mechanism of which the structural characteristics of variable cross-sectional projectile affect the stability of its trajectory is revealed.The results indicate that,when the initial impact velocity of projectile is high,the cross-sectional area at the shoulder of projectile remains consistent,and the variable cross-sectional angle is within the range of 0° to 2.5°,the velocity variations of projectiles with different cross-sectional shapes and variable cross-sectional angles during obliquely penetrating two-layer spaced steel targets are very small.For the variable cross-section projectile,a critical variable cross-section angle can be found by changing the structural characteristics of variable cross-section projectile,which makes the longitudinal displacement of the projectile penetrating the first-layer target plate basically zero.Different cross-sectional shapes of variable cross-sectional projectiles have different sensitivities to longitudinal motion and attitude deflection after penetrating the steel target at variable cross-sectional angles.The greater the ratio of long axis to minor axis of cross-sectional shape is,the greater the influence of variable cross-sectional angle on the deflection angular velocity is.Variable cross-section angle has an affect the force direction of the projectile during the process of penetrating the target,which may lead to the reversal of force on the projectile.The relevant studies have good guiding value for the optimization of structural characteristic parameters of variable cross-sectional projectile and the prediction of trajectory characteristics of variable cross-sectional projectiles during obliquely penetrating two-layer spaced steel targets.

导出引用

蒋腾 , 武海军 , 邓希旻 , 全鑫 , 董恒 , 黄风雷. 变截面弹体斜侵彻两层间隔钢靶弹道特性. 兵工学报. 2025, 46(2): 240019 https://doi.org/10.12382/bgxb.2024.0019

JIANG Teng , WU Haijun , DENG Ximin , QUAN Xin , DONG Heng , HUANG Fenglei. Study on Ballistic Characteristics of Variable Cross-section Projectile Obliquely Penetrating Two-layer Spacer Steel Target. Acta Armamentarii. 2025, 46(2): 240019 https://doi.org/10.12382/bgxb.2024.0019

中图分类号： O385

基金

国家自然科学基金项目(12072039)

0 引言

近年来,世界各国军事战略及装备发展开始聚焦速度快、突防能力强的高超声速武器。与传统飞行器外形不同,乘波体因其变截面的扁平楔形或者锥形结构设计,不仅具有高升阻比和强机动性的气动外形,而且弹体采用变截面设计还可以提高空间利用率和装填比,增强毁伤能力。相关研究表明^[1⇓⇓-4],弹道特性作为弹体重要的指标之一,其受弹体结构参数影响而发生变化,因此研究变截面弹体结构特征对斜侵彻弹道特性的影响具有重要的理论意义和工程价值。

针对传统圆截面弹体侵彻钢靶的弹道特性,国内外学者已进行了较为深入的研究。Goldsmith^[5]总结非理想条件下弹靶作用的研究内容,提出了可以从弹体剩余速度、靶板破坏模式和弹道偏转姿态等方面进行研究。Gupta等^[6-7]、Iqbal等^[8]、杜华池等^[9]开展弹体斜侵彻多层间隔钢靶的实验和数值仿真研究,得到了弹体材料、弹体入射角、弹体速度及靶板厚度对弹道特性的影响规律。国内外学者针对非圆截面弹体弹道特性研究获得了一定的成果。Dong等^[10-11]、Dai等^[12]开展椭圆截面弹体侵彻混凝土半无限靶研究,提出了刚性弹体的侵彻深度和侵彻阻力模型。Wu等^[13]基于刚体动力学和弹靶分离的思想,建立了椭圆弹体穿甲/侵彻半无限目标的三维弹道模型,并讨论了椭圆弹体的结构参数对弹道稳定性的影响。Wei等^[14-15]研究了椭圆截面弹体斜侵彻金属靶体的弹道特性,基于椭圆截面弹体侵彻弹道模型分析了椭圆截面弹体绕弹轴旋转角度、撞击速度等对侵彻弹道的影响规律。朱超等^[16]开展圆形、椭圆、非对称椭圆3种截面弹体斜侵彻条件下弹体的动态载荷特性以及结构失效条件,建立了弹体结构分析模型,给出了弹体结构强度分析方法。

在变截面弹体侵彻目标靶板弹道特性研究方面,李东伟等^[17]开展弹体斜侵彻金属靶姿态偏转研究,分析了圆截面弹体尾锥角对弹体姿态的影响规律。田泽等^[18]研究椭圆变截面弹体斜贯穿薄靶姿态偏转的机理,讨论了弹体撞击速度、初始倾角、质心位置及弹体翻滚角等参数对弹体姿态偏转的影响。邓希旻等^[19]开展上下非对称结构弹体侵彻金属薄靶的穿甲特性及靶板破坏形式的研究,分析了弹体运动特性、姿态偏转规律以及从能量耗散的角度讨论了靶板的损伤机理。

综上所述,目前对于弹体侵彻钢靶的研究,主要针对弹体材料、弹体入射角、弹体速度、靶板厚度、椭圆截面长短轴之比及质心位置等参数对弹体剩余速度、靶板破坏模式与弹体偏转等的影响,采用实验、数值模拟及理论分析取得了一定成果。但对弹体结构参数的研究仅关注等截面弹体或某一给定的变截面角度弹体,对于不同横截面形状、变截面角度对弹体穿靶后姿态偏转的影响规律不明确,变截面弹体弹靶作用的物理机制缺乏细致的分析。在实际应用中,目标物至少是两层防护结构,因此有必要开展变截面弹体侵彻两层间隔钢靶弹道特性研究。

考虑到工程实践的可行性和数值模拟的可靠性,本文先开展实验,利用获得的实验数据对数学模型参数进行修正并验模,采用数值模拟方法对实验进行补充,深入分析研究内容。为研究变截面弹体结构特征(横截面形状、变截面角度)对弹体斜侵彻两层间隔钢靶弹道特性的影响规律,本文开展椭圆截面不同变截面角度弹体斜侵彻两层间隔钢靶实验,分析弹体穿靶后的姿态变化规律,结合数值模拟方法,分析变截面弹体穿靶过程中的速度、纵向位移、偏转角和纵向加速度,揭示弹体穿靶过程的物理机制,研究结果可为变截面弹体的结构设计提供参考。

1 变截面弹体高速穿甲实验

1.1 实验准备

变截面弹体结构特征主要包括横截面形状和变截面角度。变截面弹体横截面如图1(a)所示,其中a、b分别为弹体横截面的短轴、长轴长度,以弹体长短轴之比b/a表征横截面形状,Oxy为弹体肩部横截面坐标系,坐标原点O位于等效圆中心。定义弹轴与弹体长/短轴组成的平面为长/短轴截面。变截面弹体的短轴截面如图1(b)所示,其中弹体侧壁轮廓与弹轴线的夹角λ为变截面角度,d为尾部腔直径,h为尾部腔深度。

图1 变截面弹体结构特征图

Fig.1 Structure characteristic diagram of variable cross-section projectile

Full size|PPT slide

为研究变截面弹体结构特征对斜侵彻两层间隔钢靶弹道特性的影响,设计并制备3类实验弹体,分别为椭圆等截面弹体(E)、椭圆变截面1°弹体(VE1)和椭圆变截面2.5°弹体(VE2),弹体结构参数图如图2所示。其中,各弹体的长度、头部曲率半径、弹肩处截面面积相同,并通过改变尾部腔的直径d、深度h保证各实验弹的质量相同。

图2 变截面弹体结构参数图

Fig.2 Structural parameter diagram of variable cross-section projectiles

Full size|PPT slide

弹体材料为30CrMnSiNi2A高强度钢密度为7.85g/cm³,热处理后的硬度为48.5 HRC,3类弹体的质量为50g±1g。实验弹体结构参数及实物图分别如表1、图3所示,实物图中从左至右依次分别是E型、VE1型和VE2型弹体。

表1 3类实验弹体结构参数

Table 1 Structural parameters of three types of experimental projectiles

横截面形状	弹体类型	长径比	长短轴之比	变截面角度/(°)	弹体质量/g
椭圆等截面	E	2.8	1.25	0	50.0
椭圆变截面	VE1	2.8	1.25	1	50.0
椭圆变截面	VE2	2.8	1.25	2.5	50.6

图3 实验弹体实物图

Fig.3 Views of experimental projectile

Full size|PPT slide

实验弹由φ25mm弹道炮发射,考虑到弹道炮的发射能力,着靶速度设置为850~1020m/s。当弹体的长轴平面与地面平行时,弹体在飞行过程中所受到的气动力较为均衡和稳定,减少不稳定性和偏航角度的干扰,故实验工况设置弹体长轴截面与地面平行。发射件由图4所示弹体和组合式弹托组成。为便于安装和发射时变截面弹体与弹托的分离,弹托采用三瓣式结构,两侧弹托可分开。

图4 发射件示意图

Fig.4 Schematic diagram of the launched piece

Full size|PPT slide

靶板系统包括两层水平间距350mm的Q345E钢板和45°平面镜,靶板尺寸为400mm×400mm×3mm,如图5所示。实验时弹体穿靶有火光产生,对高速摄影造成干扰,为确保高速摄影可以拍到弹体在靶间的飞行过程,靶板间距设置较大,若实验工况设置较大着角,则弹体侵彻第2层钢靶时着靶姿态较差,加剧实验的不可控性,不利于分析变截面弹体结构特征对侵彻两层间隔钢靶弹道特性研究。出于弹体的实际应用和实验研究的可行性考虑,将靶板与水平面的夹角为85°。

图5 实验靶板系统

Fig.5 Experimental target system

Full size|PPT slide

实验系统由弹道炮、靶网、靶板系统、背景布、高速摄影及回收装置组成,如图6所示,其中靶网、高速摄影分别记录弹体着靶速度及穿靶过程中的飞行姿态和弹道轨迹。

图6 实验平台示意图

Fig.6 Schematic diagram of experimental platform

Full size|PPT slide

1.2 实验结果与分析

为方便对弹体侵彻金属靶过程中的弹道特性进行分析,对相关角度进行定义和说明。弹体轴线与速度矢量之间的夹角α为攻角,弹体轴线顺时针指向速度矢量为正;速度矢量与靶板法线夹角β为着角,速度矢量顺时针指向靶板法线为正;弹体轴线与靶板法线夹角θ为姿态角,由弹体轴线指向靶板法线为正。

建立地面坐标系OXYZ,定义弹体短轴截面所在平面为竖直平面,长轴截面所在平面为水平平面,弹体在竖直平面内的运动为纵向运动。弹道炮发射方向为水平线指向,弹体轴线与水平线之间的夹角为偏转角,可分解为竖直平面内偏转角γ_v和水平平面内偏转角γ_h。如图7所示,竖直平面内由水平线顺时针指向弹体轴线γ_v为正,水平平面内由水平线逆时针指向弹体轴线γ_h为正。

图7 弹体偏转角示意图

Fig.7 Schematic diagram of deflection angle of projectile

Full size|PPT slide

根据偏转角与靶板法向量夹角的几何关系,弹体姿态角θ可表示为

c o s θ = \frac{1 - t a n γ_{v} c o t δ}{\sqrt{[1+ t a n^{2} γ_{v} + t a n^{2} γ_{h}] [1 + c o t^{2} δ]}}

(1)

式中:δ为靶板与水平面夹角。

共进行3发实验,E、VE1和VE2各1发。在测量数据时,对每发实验进行多次测量取平均值。弹体穿靶过程中的速度如表2所示。通过高速摄影获得的弹道轨迹如图8所示。由表2可知:3类弹体的速度降十分接近,3类弹体首层靶速度降约为50m/s、第2层靶速度降约为60m/s,弹体首层靶速度降小于第2层靶速度降;3类弹体第1层速度降低比率约为4.5%~5.5%,第2层速度降低比率约为6%~7.5%;VE1、VE2第1、2层速度降低比率高出E约1%,VE2第1、2层速度降低比率略高于VE1弹体,可见变截面角度对弹体速度产生的影响较小。观察图8弹体运动轨迹可知,弹体贯穿第2层靶时相较于首层靶的攻角和弹靶作用面积增大,弹体第2层靶速度降大于首层靶速度降。

表2 弹体速度统计

Table 2 Projectile velocity statistics table

序号	弹体类型	着角/(°)	首层着靶速度/ (m·s^-1)	第2层着靶速度/ (m·s^-1)	第2层出靶速度/ (m·s^-1)	首层靶速度降/ (m·s^-1)	第2层靶速度降/ (m·s^-1)	第1层速度降低比率/%	第2层速度降低比率/%
1	E	5	1034.7	987.6	929.1	47.1	58.5	4.55	5.92
2	VE1		955.7	902.4	839.2	53.3	63.2	5.58	7.00
3	VE2		872.3	822.1	760.0	50.2	61.1	5.75	7.43

图8 弹体侵彻靶板的弹道轨迹图

Fig.8 Trajectory diagram of projectile penetrating target

Full size|PPT slide

弹体出入靶板的偏转角、攻角及姿态角如表3所示。表3中:

γ_{v_{0}}

、

γ_{h_{0}}

、α₀和θ₀分别为靶前竖直平面内偏转角、水平平面内偏转角、攻角及姿态角数据;

γ_{v_{1}}

、

γ_{h_{1}}

、α₁和θ₁为靶后竖直平面内偏转角、水平平面内偏转角、攻角及姿态角数据;Δγ_v、Δγ_h、Δα和Δθ为竖直平面内偏转角、水平平面内偏转角、攻角及姿态角数据改变量。由表3可知,当3类弹体初始偏转角和攻角在±5°内、姿态角小于8°时,穿靶过程中弹体逆时针转动,偏转角逐渐增大,且随着侵彻层数的增加,弹体偏转角改变量显著提升。上述结果表明,当变?孛娼嵌仍?°~2.5°内时,椭圆变截面角度的大小未改变弹体在竖直平面内的转动方向。

表3 弹体穿甲过程姿态统计

Table 3 Attitude statistics table of projectile during armor-piercing process (°)

弹体类型	着角	靶板编号	偏转角						攻角			姿态角
弹体类型	着角	靶板编号	$γ_{v_{0}}$	$γ_{v_{1}}$	Δγ_v	$γ_{h_{0}}$	$γ_{h_{1}}$	Δγ_h	α₀	α₁	Δα	θ₀	θ₁	Δθ
E	5	1	3	1	-2	0	0	0	-3	-3	0	8.0	5.1	-2.9
E		2	-4	-8	-4	0	0	0	7	13	6	1.0	9.4	8.3
VE1		1	-5	-7	-2	6	12	6	5	6	1	6.0	13.0	7.0
VE1		2	-12	-34	-22	12	38	26	8	26	18	13.6	37.0	23.4
VE2		1	-3	-7	-4	5	4	-1	3	9	6	5.3	12.2	6.9
VE2		2	-12	-27	-15	4	4	0	10	22	12	8.0	28.3	20.3

E型弹体斜贯穿两层间隔靶后竖直平面内偏转角变化11°,水平平面内偏转角变化2°;VE型斜贯穿两层间隔靶后竖直平面内偏转角变化24°~29°,水平平面内偏转角变化1°~32°。对比3类弹体贯穿首层靶后的偏转角改变量,可以看到竖直平面内偏转角改变量Δγ_v依次排序为VE2>VE1=E;水平平面内偏转角改变量Δγ_h依次排序为VE1>VE2>E;对比3类弹体贯穿第2层靶后的偏转角改变量,Δγ_v依次排序为VE1>VE2>E;Δγ_h依次排序为VE1>VE2=E。对比3类弹体初始着靶姿态可知,椭圆等截面弹体以初始正偏转角和负攻角侵彻两层间隔钢靶时弹道稳定性较好,椭圆变截面1°弹体抗偏转能力弱于椭圆变截面2.5°弹体。

弹体贯穿首层靶板后,底推对靶板造成了二次损伤,导致首层靶的最终形貌无法反映弹体与靶板的单独作用模式。因此通过分析第2层靶板的破坏形貌,研究3类弹体与靶板的作用模式,第2层靶板的破坏形貌如图9所示。由图9和图10可知,靶板的破坏模式主要以延性扩孔、剪切冲塞、挤压变形为主;弹体高速斜侵彻靶板时,弹头下侧首先接触靶板发生作用,弹头下侧发生明显侵蚀。弹靶作用模式依次为:靶板与弹体接触边缘首先发生延性扩孔、局部绝热剪切、形成冲塞块,靶板发生冲塞后,弹体继续前进并挤压靶板破口。由于弹体姿态偏转及上下运动趋势,导致靶板破口受力不均匀,当弹体姿态偏转较小时,靶板两侧受弹体正向挤压作用弱,破口没有出现撕裂现象,如图9中E型弹体工况;当弹体姿态偏转严重时,靶板下侧受弹体正向挤压作用而产生花瓣翻转撕裂、甚至根部断裂的现象,如图9中VE1型弹体工况。对比3类弹体的靶板破坏模式可知,椭圆变截面1°弹体贯穿第2层靶过程中的受力不对称性大于椭圆等截面弹体和椭圆变截面2.5°弹体,结合椭圆等截面弹体穿甲结果可知,椭圆变截面角度特征会增大弹体的受力不对称性,但椭圆变截面角度与受力不对称性呈非线性相关关系。

图9 第2层靶板破坏形貌图

Fig.9 Failure topography of the second layer target

Full size|PPT slide

图10 回收弹体及冲塞块图

Fig.10 Recovered projectiles and plate plugs

Full size|PPT slide

2 数值模拟仿真

2.1 仿真模型的建立

数值模拟采用Abaqus/Explicit有限元软件,采用8节点减缩单元C3D8R,选用g-cm-μs单位制。仿真计算弹体尺寸与实验尺寸一致,考虑到高速穿甲过程靶板以局部响应为主^[19],故靶板尺寸设为10倍弹体直径,针对弹靶对称结构特性,为提高计算效率,建立1/2有限元模型进行计算分析。在靶板边界设定固定边界条件,限制靶板沿弹体运动方向位移,弹靶有限元模型如图11所示。网格尺寸对计算精度有较高的影响,因此以E型弹体1020m/s初速、5°着角条件下斜贯穿两层3mm Q345E钢板为例,对比了加密区网格尺寸对计算结果的影响,如图12所示。由图12可见:加密区网格尺寸为0.2~0.6mm时,弹体剩余速度变化不大。考虑到计算精度和计算耗时,因此选择0.5mm作为加密区网格尺寸。为控制计算效率和计算精度,对靶板中心130mm×65mm区域进行网格细化,非中心区域采用渐变网格进行过渡,减少网格数量,靶板非加密区网格尺寸为4mm,弹体非加密区网格尺寸为0.8mm。弹靶采用通用接触算法,确保能准确描述穿甲过程中弹体与靶板的变形破坏行为。

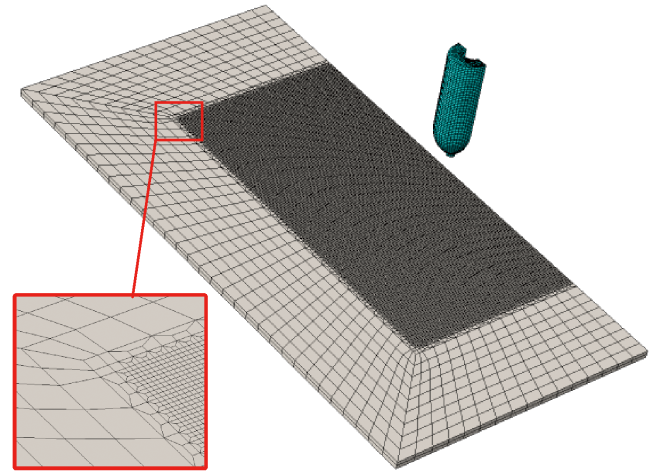
图11 弹靶有限元模型示意图

Fig.11 Schematic diagram of finite element model of projectile and target

Full size|PPT slide

图12 网格敏感性验证

Fig.12 Grid sensitivity verification

Full size|PPT slide

对实验弹体回收后发现,弹体头部有侵蚀,如图10所示,表明弹体与靶板作用过程中产生明显的塑性变形和动态损伤,因此在数值模拟中弹体选用变形体。参考相关文献^[9,20-21],弹靶采用J-C(Johnson-Cook)本构模型表征,弹体材料参数如表4所示,靶板材料参数如表5所示。

表4 30CrMnSiNi2A材料模型参数

Table 4 30CrMnSiNi2A material model parameters

ρ/(g·cm^-3)	E/GPa	v	T_r	T_m	$\overset{\cdot}{ε}$ ₀/s^-1	χ	m	c_p/(J·kg^-1·K^-1)
7.85	210	0.3	294	1760	2.1×10^-3	0.9	1	452
A/MPa	B/MPa	n	C	C₁	C₂	C₃	C₄	C₅
1269	810	0.479	0.040	0.248	2.392	0.317	5.504	-4.161

注:ρ为密度,E为弹性模量,v为泊松比, χ为塑性功转热因子,c_p为定压比热容,C₁~C₅为待定参数。

表5 Q345E材料模型主要参数

Table 5 Main parameters of Q345E material model

ρ/(g·cm^-3)	E/GPa	v	A/MPa	B/MPa	n
7.85	206	0.28	355	930	0.496
m	D₁	D₂	D₃	D₄	D₅
1.0	0.2	1.16	-1.22	-0.0234	1.5

注:ρ为密度,E为弹性模量,v为泊松比,D₁~D₅为J-C失效模型参数。

Johnson-Cook本构模型表达式为

σ = (A + B ε^{n}) [1 + C l n (1 + \frac{\dot{ε}}{{\dot{ε}}_{0}})] (1 - T^{* m})

(2)

式中:σ为等效应力;A为静态屈服应力;B为硬化系数;C为应变率参数;ε为等效塑性应变;n为硬化指数;

\overset{\cdot}{ε}

为有效塑性应变率;

\overset{\cdot}{ε}

₀为参考应变率;T^*=(T-T_r)(T_m-T_r),T为材料环境温度,T_r为室温,T_m为材料熔化温度,m为软化指数,。

弹体失效模型采用Bao-Wierzbicki提出的失效应变ε_f与应力三轴度η关系模型,表达式如下:

ε_{f} = \{\begin{array}{l} \infty, & η \leq - \frac{1}{3} \\ \frac{C_{1}}{1 + 3 η}, & - \frac{1}{3} η \leq 0 \\ C_{2} η + C_{1}, & 0 η \leq η_{0} \\ C_{3} + C_{4} e x p (C_{5} η), & η > η_{0} \end{array}

(3)

式中:C₁~C₅为待定参数;η₀为拉剪应力状态与单轴拉伸-高应力三轴度状态相交位置的应力三轴度。依据文献[22]可知:C₁=0.248,C₂=2.392,C₃=0.317,C₄=5.504,C₅=-4.161,η₀=0.424,见表4。靶板采用J-C(Johnson-Cook)失效模型,详细参数见表5。

2.2 仿真与实验对比分析

基于2.1节中的有限元模型和仿真参数,对实验中的E型弹体工况进行数值仿真,获得弹体贯穿靶板后的靶板破坏形貌及穿靶过程中的弹道轨迹、速度和偏转角时程曲线,如图13~图16所示,速度和偏转角实验与仿真计算对比如表6、表7所示。弹体贯穿首层靶板后,随进的弹托会影响首层靶的破坏形貌,因此验证仿真有效性时仅讨论第2层靶板。由图13可见,弹孔形状呈椭圆状,延性扩孔形成的唇沿在弹孔四周堆积,靶板背面在椭圆长轴方向受环向拉伸作用形成I型裂纹,数值仿真得到的靶板破坏形貌与实验后的靶板破坏形貌具有一致性。

图13 仿真靶板破坏形貌图

Fig.13 Simulation target failure topography

Full size|PPT slide

图14 仿真与实验弹道轨迹图

Fig.14 Simulation and experiment ballistic trajectory diagram

Full size|PPT slide

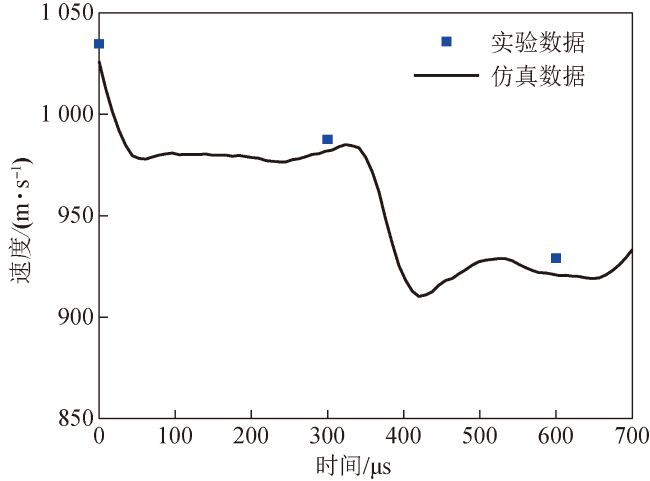
图15 速度时程曲线仿真与实验数据对比

Fig.15 Speed-time curve simulation and experimental data comparison

Full size|PPT slide

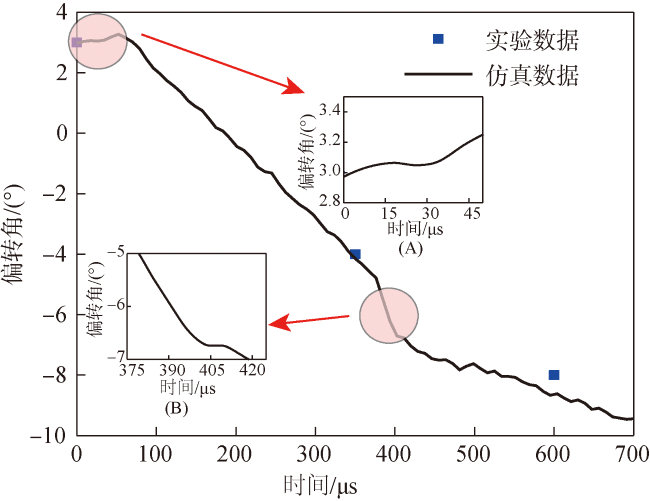
图16 偏转角时程曲线仿真与实验数据对比

Fig.16 Deflection angle-time curve simulation and experimental data comparison

Full size|PPT slide

表6 实验与仿真速度对比

Table 6 Experimental and simulated speeds

弹体类型	实验速度/(m·s^-1)			仿真速度/(m·s^-1)			相对误差/%
E	首层着靶速度	靶间速度	第2层出靶速度	首层着靶速度	靶间速度	第2层出靶速度	靶间速度	第2层出靶
E	1034.7	987.6	929.1	1034.7	978.1	916.1	0.96	1.41

表7 实验与仿真偏转角对比

Table 7 Experimental and simulated deflection angles

弹体类型	实验偏转角/(°)			仿真角度/(°)			相对误差/%
E	首层着靶角度	第2层着靶角度	第2层出靶角度	首层着靶角度	第2层着靶角度	第2层出靶角度	第2层着靶	第2层出靶
E	3	-4	-8	3	-4.19	-8.48	4.53	5.66

由图14可以看出,弹体出首层靶后呈向下、逆时针旋转运动趋势,侵彻第2层时弹体继续向下运动、逆时针旋转,穿甲过程结束后,弹体由低头着靶(正偏转角)变为抬头出靶(负偏转角)。结合图15和表6可以看出,弹体贯穿首层靶后,弹体速度下降约50m/s;贯穿第2层靶后,弹体速度下降约60m/s。弹体靶间速度和第2层出靶速度实验与仿真相对误差小于2%。由图16和表7可见,弹体贯穿首层靶后,偏转角变化7°;贯穿第2层靶后,偏转角变化4°。弹体第2层着靶偏转角和第2层出靶偏转角实验与仿真相对误差小于6%。综上所述可知,模拟结果与实验结果吻合较好,可以认为2.1节中有限元模型和仿真参数的设置科学合理,能够在一定程度上反映实验结果。

2.3 弹体斜侵彻两层间隔钢靶过程分析

为研究变截面结构特征对弹体穿甲特性的影响,需要明确分析弹体斜侵彻两层间隔钢靶物理过程的方法。为此,基于图16~图18给出的E型弹体工况偏转角、纵向加速度及纵向位移时程曲线数值仿真结果,将E型弹体工况穿靶过程划分为两个阶段进行物理机制分析,如图19所示。

由图17可见,E型弹体工况的穿靶过程可分为4个时间区域,T₁和T₃分别对应弹体侵彻首层靶、第2层靶过程,T₂和T₄分别对应弹体在靶间及靶后的飞行过程。在T₁和T₃时间区域内,纵向加速度各出现两次峰值,①和③、②和④分别对应弹体质心前部分穿靶阶段和弹体质心后部分穿靶阶段,如图19所示。

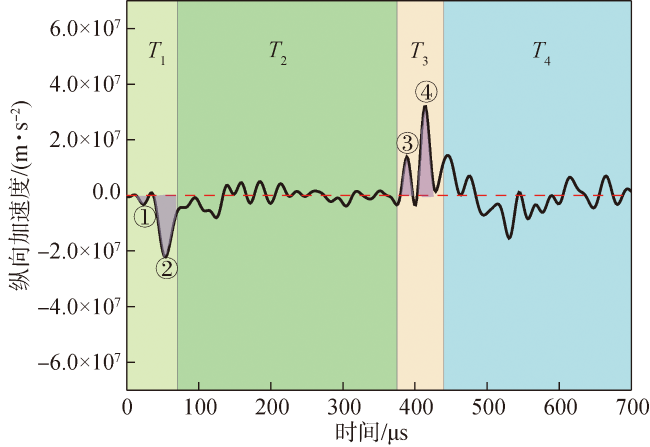
图17 E型弹体纵向加速度-时程曲线

Fig.17 Longitudinal acceleration-time curve of E-type projectile

Full size|PPT slide

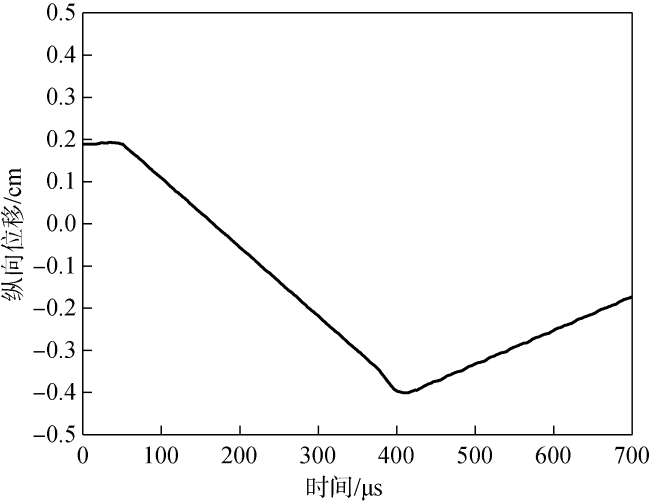
图18 E型弹体纵向位移-时程曲线

Fig.18 Longitudinal displacement-time curve of E-type projectile

Full size|PPT slide

图19 弹体穿靶不同阶段图

Fig.19 Different stages of projectile penetration

Full size|PPT slide

由于E型弹体工况着靶前呈低头姿态,头部上侧作用面积大,导致弹体头部承受向下的作用力。弹体纵向加速度在此刻达到峰值①,此阶段属于弹体质心前部分穿靶,弹靶作用力对弹体质心产生顺时针力矩,弹体偏转角增大,如图16中局部放大图A所示。随着弹体进一步侵彻靶板,靶板下侧对弹体头部的向上作用力逐渐增大,弹体纵向加速度逐渐减小。弹体头部穿靶后,弹体继续向前运动,因撞击时间短,弹体偏转较小,靶板上侧与弹体仍保持接触,靶板下侧由于惯性作用与弹体逐渐分离,如图19(b)所示。弹体纵向加速度在此刻达到峰值②,此阶段属于弹体质心后部分穿靶,弹靶作用力对弹体质心产生逆时针力矩,弹体偏转角减小,如图16所示。由图17可见,弹体纵向加速度峰值①和②均小于零,弹体整体受靶板的向下作用力,故弹体贯穿首层靶后,纵向位移减小,呈向下运动趋势,如图18所示。弹体纵向加速度峰值②远大于峰值①,纵向加速度峰值②出现的时刻处于弹体质心后部分穿靶阶段,弹体整体受靶板的逆时针力矩作用,弹体贯穿首层靶后,呈逆时针旋转运动趋势。弹体贯穿首层靶板后进入靶间飞行阶段,在此阶段弹体纵向加速度趋于零,偏转角和纵向位移线性减小。

弹体侵彻第2层靶与弹体侵彻首层靶过程类似,弹体纵向加速度峰值③和④大于0,弹体整体受靶板的向上作用力,故弹体贯穿第2层靶后,纵向位移增大,呈向上运动趋势,如图18所示。纵向加速度在弹体质心前部分穿靶阶段达到峰值③,弹靶作用力对弹体产生逆时针力矩作用,弹体偏转角减小速度加快,如图16中局部放大图B所示。纵向加速度在弹体质心后部分穿靶阶段达到峰值④,弹靶作用力对弹体产生顺时针力矩作用,弹体偏转角减小速度放缓,如图16所示。由于偏转角增大,导致弹靶作用面积增大,进而弹体受到的阻力增大,故弹体斜侵彻第2层靶板的峰值大于第1层靶板,这与弹体侵彻靶板时的速度降规律表现一致。

2.4 变截面弹体结构特征对弹道特性影响分析

在高速穿甲实验及相关数值仿真的基础上,分析横截面形状及变截面角度对弹道特性的影响,实验弹相关参数如表8所示。弹体初速为1020 m/s,两层靶板厚度均为3mm,靶板间距为350mm,着角为5°。

表8 变截面弹体参数

Table 8 Statistical table of variable cross-section projectile parameters

序号	横截面形状	变截面角度/ (°)	编号	长短轴之比	弹长/ mm	弹体质量/g
1	圆等截面	0	C	1	42	50.0
2	圆等截面	1	VC1
3	圆等截面	2.5	VC2
4	椭圆等截面	0	E	1.25
5	椭圆变截面	1	VE1
6	椭圆变截面	2.5	VE2

弹体在所设置的条件下斜侵彻两层间隔钢靶的数值模拟示意图如图20所示。各类弹体速度、纵向位移、偏转角和纵向加速度时程曲线如图21~图24所示。由图21可见,6类弹体速度呈阶梯式衰减变化趋势,弹体速度降没有明显差异,弹型以初速1020m/s贯穿首层3mm间隔钢靶后,弹体速度降约为50m/s;贯穿第2层3mm靶板后,速度降约为60m/s。当弹体初始撞击速度较大、弹肩处横截面面积一致时,横截面形状和变截面角度对穿靶过程中速度产生的影响很小。

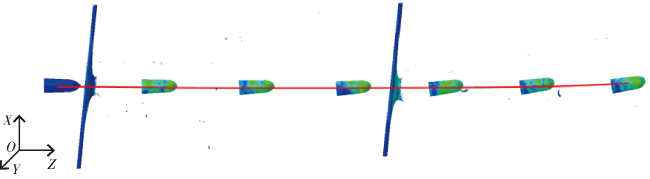
图20 弹体侵彻双层间隔钢靶数值模拟示意图

Fig.20 Schematic diagram of numerical simulation of projectile penetrating double-layer spaced steel target

Full size|PPT slide

图21 弹体速度时程曲线图

Fig.21 Projectile velocity-time curve

Full size|PPT slide

图22 弹体纵向位移时程曲线图

Fig.22 Longitudinal displacement-time curves of projectiles

Full size|PPT slide

图23 弹体偏转角时程曲线图

Fig.23 Deflection angle-time curves of projectiles

Full size|PPT slide

图24 不同截面弹体纵向加速度时程曲线图

Fig.24 Longitudinal acceleration-time curves of projectiles with different sections

Full size|PPT slide

各实验弹穿靶过程中的纵向位移如图22所示。由图22(a)可知,6类弹体在贯穿两层间隔钢靶后,纵向位移增大,呈向上的运动趋势,700μs后纵向位移依次排序为E<C<VE1<VC1<VE2<VC2。由图22(b)可知,圆截面弹体在贯穿首层钢靶后具有不同的运动趋势,C型弹体向下运动,VC2型弹体向上运动,VC1型弹体基本保持直线运动。由图22(c)可见,椭圆截面弹体贯穿首层钢靶后,3类弹体均具有向下的运动速度。由图22(d)可见,同一横截面形状下,变截面弹体在贯穿第2层钢靶后,变截面角度越大,弹体纵向位移和运动速度越大。

对比6类弹体纵向位移结果,在本文设置的着靶条件下,横截面形状和变截面角度不影响弹体贯穿两层间隔钢靶后的纵向位移变化趋势。对于变截面弹体,可能存在一个使得弹体贯穿首层靶板后纵向位移方向发生改变的临界变截面角度,小于该临界变截面角度时,弹体贯穿首层靶后向下运动,反之向上运动。对比椭圆截面弹体和圆截面弹体可知,该临界角度的存在与否及大小和横截面形状关系密切,在本文设置的着靶条件下,当横截面形状为圆形时,此临界角度为1°。变截面角度会加剧弹体斜侵彻两层间隔钢靶后的纵向位移偏转特性,圆截面弹体贯穿首层靶后的纵向位移方向更易受到变截面角度影响;椭圆截面弹体贯穿第2层靶后纵向运动速度更易受到变截面角度影响。

由于数值仿真采用1/2模型,故仅对弹体穿靶过程中竖直平面内的偏转角进行分析。各实验弹穿靶过程中的偏转角如图23所示。由图23(a)可知,6类弹体在贯穿两层间隔钢靶后,偏转角减小,呈抬头的运动趋势,700μs后偏转角绝对值依次排序为E<C、VC2<VC1<VE2<VE1。由图23(b)、图23(c)、图23(d)可以得出,弹体贯穿首层钢靶后,VC1型和VE1型弹体角速度基本一致,VC2型和VE2型弹体角速度基本一致,且变截面1°弹体获得的角速度较大。弹体贯穿第2层钢靶后,C型和VC1型弹体角速度基本不变,VC2型弹体角速度变小。VE1型和VE2型弹体角速度变大,E型弹体角速度基本不变。

对比6类弹体偏转角结果,在设置的着靶条件下,横截面形状和变截面角度不影响弹体贯穿两层间隔钢靶后的偏转角变化趋势。对于变截面弹体,变截面角度对弹体偏转角及角速度的影响是非线性的,同一变截面角度对不同横截面形状弹体贯穿首层钢靶后角速度的影响程度基本一致;对不同横截面形状弹体贯穿第2层钢靶后角速度的影响不同,横截面形状的长短轴之比越大,变截面角度对偏转角速度的影响越大。

结合2.3节中的弹体斜侵彻两层间隔钢靶分析方法,提取6类弹体纵向加速度时程曲线,见图24。为方便观察弹体纵向加速度的方向,在图24中用红色虚线表示纵向加速度为零,用粉色填充曲线与红色虚线之间的面积,当曲线位于红色虚线下方时,表示纵向加速度为负,反之为正。

由图24可知,在初始偏转角、攻角为0°的着靶条件下,弹体穿靶按时间可分为3个阶段。

第一阶段:弹体初始穿靶时,由于弹体着角较小,弹体头部上下侧受力基本对称,如图25(a)所示,时间范围大约为0~20μs,此时弹体姿态无明显变化。

图25 弹体穿靶过程示意图

Fig.25 Schematic diagram of projectile penetration process

Full size|PPT slide

第二阶段:随着弹体继续前进,此时弹体下侧处于弹肩或弹身穿靶过程,弹体上侧仍处于弹头穿靶过程,弹体上下侧出现受力不对称现象,各类型弹体在此时出现不同类型的姿态变化趋势。对比图24可知,当弹体为等截面时,弹体下侧受力大于上侧,如图25(b)所示。当弹体变截面角度为1°时,弹体受向下作用力大于向上作用力,受力分析如图25(c)所示。当圆截面弹体变截面角度为2.5°时,弹体受向上作用力大于向下作用力,与图25(b)所示类似。对于等截面弹体,此阶段时间范围大约为20~40μs,由于变截面角度影响,变截面弹体与靶板持续接触,变截面弹体在第二阶段受力不均匀现象出现较晚,且变截面角度引起的受力不对性增大,VC1型、VE1型和VE2型弹体尤为明显。

第三阶段:在穿靶过程中,弹体在受到一侧的作用力后,会向对侧移动。在此过程中,对于圆等截面弹体,靶板下侧因惯性作用与弹体逐渐分离,向下作用力大于向上作用力,弹体整体承受向下的作用力,随着穿甲过程的结束,弹体受力最终趋于零,如图25(d)所示。由于变截面角度的存在,变截面弹体与靶板下侧未出现分离现象,且圆变截面1°弹体受第二阶段作用力影响,向对侧移动,如图25(e)所示。与圆等截面弹体相比,椭圆截面弹体在穿靶过程容易偏转,弹体受力出现上下波动的现象。对于椭圆变截面弹体,变截面角度减弱了弹体在此过程中的波动现象,此阶段时间范围大约为40~60μs。与弹体贯穿首层靶板过程分析方法类似,但需考虑弹体贯穿首层靶板产生的攻角影响,此处不再赘述弹体贯穿第2层靶板的过程。

对比6类弹体纵向加速度结果得,相较于圆截面弹体,椭圆截面弹体在穿靶第三阶段受力易波动,变截面角度会减小波动幅值。变截面角度会影响弹体的受力方向,对于圆截面弹体,变截面角度为1°时,弹体穿靶受力出现反转现象;对于椭圆截面弹体,变截面1°和2.5°弹体受力都出现了反转现象。

3 结论

本文开展了变截面弹体斜侵彻两层间隔钢靶实验研究,通过高速摄影系统获得了弹体的速度、姿态偏转等弹道参数。结合数值仿真分析了横截面形状和变截面角度对速度、纵向位移、偏转角和纵向加速度等弹道参数的影响规律。基于弹体纵向加速度时程曲线分析了变截面弹体结构特征对穿靶过程的影响,揭示了弹靶作用的物理机制。得到主要结论如下:

1)当弹体初始撞击速度较大、弹肩处横截面面积一致及变截面角度在0°~2.5°范围内时,不同横截面形状和变截面角度弹体在斜侵彻两层间隔钢靶过程中的速度变化差异很小。

2)对于变截面弹体,可以通过改变变截面结构特征(横截面形状、变截面角度)找到一个使得弹体贯穿首层靶板后纵向位移基本为零的临界变截面角度。在设置的着靶条件下,当横截面形状为圆形时,此临界变截面角度为1°。变截面角度会加剧弹体贯穿两层间隔钢靶后的姿态偏转,但对偏转角的影响是非线性的。

3)不同横截面形状的变截面弹体受变截面角度对贯穿钢靶后纵向运动、姿态偏转的敏感程度不同。圆截面弹体贯穿首层靶后的纵向位移方向更易受到变截面角度影响,椭圆截面弹体贯穿第2层靶后纵向运动速度更易受到变截面角度影响,横截面形状的长短轴之比越大,变截面角度对偏转角速度的影响越大。

4)变截面角度会影响弹体穿靶过程中的受力方向,可能导致弹体受力出现反转现象。对于圆截面弹体,变截面角度为1°时,弹体穿靶受力出现反转现象,对于椭圆截面弹体,变截面1°和2.5°弹体受力都出现了反转现象。

参考文献

原文顺序 | 文献年度倒序 | 文中引用次数倒序

[1]	BACKMAN M E, GOLDSMITH W. The mechanics of penetration of projectiles into targets[J]. International Journal of Engineering Science, 1978, 16(1):1-99. 本文引用 [1]

[2]	KPENYIGBA K M, JANKOWIAK T, RUSINEK A, et al. Effect of projectile nose shape on ballistic resistance of interstitial-free steel sheets[J]. International Journal of Impact Engineering, 2015, 79:83-94. 本文引用 [1]

[3]

葛超, 董永香, 陆志超, 等. 弹丸头部对斜侵彻弹道偏转影响研究[J]. 兵工学报, 2015, 36(2):255-262.

https://doi.org/10.3969/j.issn.1000-1093.2015.02.010

摘要

通过对不同头部形状与组合材料的弹头对中厚钢靶的斜侵彻弹道对比研究，获得了尖卵形、截卵形与内凹截卵形，以及不同截卵位置、弹头长度和头部组合材料弹头对斜侵彻中弹道偏转的影响规律和侵彻过程中受到偏转力矩的变化规律。计算结果表明：截卵形弹弹道偏离角小，抗弹道姿态劣化的能力强，侵彻弹道相对稳定性好；弹头前端复合高密度、高硬度钨合金材料的弹丸侵彻能力强，弹道偏离角小。基于弹道侵彻过程偏转力矩与偏转角的时空演化特点，获得斜侵彻弹道偏转关联性。通过正交试验得到了影响弹道偏离角由大到小的因素分别为：弹头形状、弹头材料和弹速。研究结果可为低速弹丸与金属靶的斜侵彻弹道分析和弹丸头部设计提供一定帮助。

, DONG

Y X

, LU

Z C

, et al. Research on the influence of projectile head on oblique penetration ballistic deflection[J]. Acta Armamentarii, 2015, 36(2):255-262. (in Chinese)

本文引用 [1]

[4]	SENTHIL K, IQBAL M A. Effect of projectile diameter on ballistic resistance and failure mechanism of single and layered aluminum plates[J]. Theoretical and Applied Fracture Mechanics, 2013, 67-68(5):53-64. 本文引用 [1]

[5]	GOLDSMITH W. Non-ideal projectile impact on targets[J]. International Journal of Impact Engineering, 1999, 22(2):95-395. 本文引用 [1]

[6]	GUPTA N K, MADHU V. An experimental study of normal and oblique impact of hard-core projectile on single and layered plates[J]. International Journal of Impact Engineering, 1997, 19(5):395-414. 本文引用 [1]

[7]	GUPTA N K, MADHU V. Normal and oblique impact of a kinetic energy projectile on mild steel plates[J]. International Journal of Impact Engineering, 1992, 12(3):333-343. 本文引用 [1]

[8]	IQBAL M A, SENTHIL K, MADHU V, et al. Oblique impact on single,layered and spaced mild steel targets by 7.62 AP projectiles[J]. International Journal of Impact Engineering, 2017, 110:26-38. 本文引用 [1]

[9]

杜华池, 张先锋, 刘闯, 等. 弹体斜侵彻多层间隔钢靶的弹道特性[J]. 兵工学报, 2021, 42(6):1204-1214.

https://doi.org/10.3969/j.issn.1000-1093.2021.06.010

摘要

为分析弹体斜侵彻多层间隔靶的弹道特性，开展典型卵形弹体不同入射角侵彻多层间隔钢靶试验和数值模拟研究。利用有限元软件LS-DYNA建立弹体斜侵彻多层间隔钢靶数值仿真模型，分析弹体斜侵彻多层间隔钢靶作用过程，得出弹体入射角、弹体速度、靶体厚度及弹体变形对多层钢靶侵彻弹道特性的影响规律并进行了试验验证。结果表明：弹体入射角越大，侵彻弹道偏转越大；初始速度越大，弹体斜侵彻多层间隔钢靶偏转角度越小，且速度对偏转角的影响幅度随速度增大呈减小趋势；随着靶体厚度增加，弹体斜侵彻多层间隔钢靶弹道由整体向下偏转转变为整体向上偏转；靶体厚度对偏转角的影响幅度随靶体厚度增大呈增大趋势；刚性弹体斜侵彻多层间隔钢靶弹道偏转角度比变形弹小。

H C

, ZHANG

X F

, LIU

, et al. Ballistic characteristics of projectile oblique penetration into multi-layer spaced steel targets[J]. Acta Armamentarii, 2021, 42(6):1204-1214. (in Chinese)

本文引用 [2]

[10]	DONG H, LIU Z H, WU H J, et al. Study on penetration characteristics of high-speed elliptical cross-sectional projectiles into concrete[J]. International Journal of Impact Engineering, 2019, 132:103311. 本文引用 [1]

[11]	DONG H, WU H J, LIU Z H, et al. Penetration characteristics of pyramidal projectile into concrete target[J]. International Journal of Impact Engineering, 2020, 143:103583. 本文引用 [1]

[12]

DAI

X H

, WANG

K H

, LI

M R

, et al. Rigid elliptical cross-section ogive-nose projectiles penetration into concrete targets[J]. Defence Technology, 2021, 17(3):800-811.

https://doi.org/10.1016/j.dt.2020.05.011

本文引用 [1] 摘要

The elliptical cross-section ogive-nose projectile (ECOP) has recently attracted attention because it is well suited to the flattened shape of earth-penetrating weapons. However, the penetration performance of ECOPs has not been completely understood. The objective of this study was to investigate the penetration performance of ECOPs into concrete targets using a theoretical method. A general geometric model of ECOPs was introduced, and closed-form penetration equations were derived according to the dynamic cavity-expansion theory. The model was validated by comparing the predicted penetration depths with test data, and the maximum deviation was 15.8%. The increment in the penetration depth of the ECOP was evaluated using the proposed model, and the effect of the major–minor axis ratio on the increment was examined. Additionally, the mechanism of the penetration-depth increment was investigated with respect to the caliber radius head, axial stress, and resistance. © 2020 The Authors

[13]	WU H J, DENG X M, DONG H, et al. Three-dimensional trajectory prediction and analysis of elliptical projectile[J]. International Journal of Impact Engineering, 2023, 174:104497. 本文引用 [1]

[14]	WEI H Y, ZHANG X F, LIU C, et al. Oblique penetration of ogive-nosed projectile into aluminum alloy targets[J]. International Journal of Impact Engineering, 2021, 148:103745. 本文引用 [1]

[15]	WEI H Y, ZHANG X F, LIU C, et al. A three-dimensional penetration trajectory model for ogive-nosed projectile into metal targets[J]. International Journal of Impact Engineering, 2021, 157:103998. 本文引用 [1]

[16]	朱超, 张晓伟, 张庆明, 等. 弹体斜侵彻双层钢板的结构响应和失效研究[J]. 爆炸与冲击, 2023, 43(9):140-154. ZHU C, ZHANG X W, ZHANG Q M, et al. Structural response and failure study of projectile oblique penetration of double-layer steel plate[J]. Explosion and Impact, 2023, 43(9):140-154. (in Chinese) 本文引用 [1]

[17]

李东伟, 刘俞平, 王筱锋, 等. 弹形参数对战斗部斜穿甲姿态偏转影响研究[J]. 兵器装备工程学报, 2021, 42(9):40-44.

D W

, LIU

Y P

, WANG

X F

, et al. Research on the influence of projectile shape parameters on the attitude deflection of oblique armor piercing of the warhead[J]. Chinese Journal of Weapon Equipment Engineering, 2021, 42(9):40-44. (in Chinese)

本文引用 [1]

[18]

田泽, 王浩, 武海军, 等. 椭圆变截面弹体斜贯穿薄靶姿态偏转机理[J]. 兵工学报, 2022, 43(7):1537-1552.

https://doi.org/10.12382/bgxb.2021.0367

摘要

随着新型武器平台的发展，具有良好平台适应性、高升阻比及隐身性能等特点的异形截面（椭圆形及变截面椭圆形）战斗部开始受到广泛关注。为探究椭圆变截面弹体斜贯穿薄靶机理与姿态偏转规律，对3种不同截面（圆形、椭圆形、变截面椭圆形）弹体斜贯穿双层945舰船薄钢板实验过程及结果进行整理与分析，根据椭圆变截面弹体贯穿过程、靶板破坏失效模式与弹体受力特征，将贯穿过程分为弹体头部压入阶段、弹体头部贯穿阶段、过渡阶段与弹身贯穿阶段。基于能量守恒、虚功原理分阶段分析弹体受力特征，建立弹体姿态偏转理论模型。通过对已有实验和数值模拟结果与理论模型所得结果进行对比，验证理论模型的可靠性。采用该理论模型着重讨论弹体撞击速度、初始倾角、质心位置、弹体翻滚角及椭圆截面长短轴之比等参数对椭圆变截面弹体姿态偏转的影响。结果表明：随着椭圆变截面弹体初始撞击速度的增加，弹体姿态偏转角度呈现指数型减小趋势；随着椭圆变截面弹体初始倾角的增大，弹体姿态偏转量增大；随着椭圆变截面弹体质心位置的后置，弹体姿态偏转角度增大；椭圆变截面弹体以不同的翻滚角撞击靶板时，弹体姿态偏转角度不同，γpt=0°较γpt=90°时弹体姿态偏转角度更大；当γpt=0°时，椭圆变截面弹体椭圆截面长短轴之比增大，弹体姿态偏转角度随之增大；当γpt=90°时，规律则相反。

TIAN

, WANG

, WU

H J

, et al. Attitude deflection mechanism of elliptical variable-section projectile obliquely penetrating thin target[J]. Acta Armamentarii, 2022, 43(7):1537-1552. (in Chinese)

本文引用 [1]

[19]

邓希旻, 田泽, 武海军, 等. 上下非对称结构弹体侵彻金属薄板的特性及薄板破坏形式[J]. 兵工学报, 2023, 44(12):3836-3850.

https://doi.org/10.12382/bgxb.2022.0724

摘要

为支撑超高声速导弹终点毁伤理论设计,适应异型弹体穿甲力学基础理论发展需求,非对称异型弹体贯穿金属薄板的穿甲特性及靶板损伤机理是当前亟需解决的关键科学问题。开展上下非对称结构异型弹体正/斜贯穿多层间隔921A薄钢板实验,基于Abaqus/Explicit、VUMAT和Python子程序开展数值模拟研究,分析弹体速度变化及偏转特性,结合靶板破坏形貌和能量耗散分析靶板损伤机理,讨论了研究结果在实际工程应用中的适用性。研究结果表明:上下非对称结构异型弹体具有维持弹体姿态稳定的特点,初速低于600m/s时速度降和弹道极限随倾角的增加而增大,靶板破坏模式以剪切冲塞、瓣裂和整体横向变形主导,初速高于600m/s时同初始倾角的弹道极限曲线重合,无量纲速度降随初速增加而降低,靶板破坏模式向延性扩孔、瓣裂和破碎转变;靶板塑性变形时切向塑性功占比最大、环向塑性功最小、轴向和径向塑性功相近,高速侵彻过程中靶板碎片动能为塑性功的25%~50%;基于几何相似的缩比模型可反映原型弹体高速穿甲时的速度变化情况及靶板的毁伤特性;研究成果可为异型弹体高速穿甲的弹靶响应及阻力特性的理论建模提供物理认识及数据支撑。

DENG

X M

, TIAN

, WU

H J

, et al. Characteristics of upper and lower asymmetric structural projectiles penetrating metal thin plates and the failure forms of thin plates[J]. Acta Armamentarii, 2023, 44(12):3836-3850. (in Chinese)

本文引用 [2]

[20]	李磊. 不同硬度30CrMnSiNi2A钢动态本构与损伤参数研究[D]. 南京: 南京理工大学, 2017. LI L. Study on dynamic constitutive and damage parameters of 30CrMnSiNi2A steel with different hardness[D]. Nanjing: Nanjing University of Science and Technology, 2017. (in Chinese) 本文引用 [1]

[21]	WANG Y A, WANG Z, LIANG S H, et al. Experimental and numerical study on the failure modes of ship stiffened plate structure under projectile perforation[J]. International Journal of Impact Engineering, 2023, 178:104590. 本文引用 [1]

[22]	余万千, 郁锐, 崔世堂, 等. 考虑应力三轴度影响的30CrMnSiNi2A钢韧性断裂研究[J]. 爆炸与冲击, 2021, 41(3):47-54. YU W Q, YU R, CUI S T, et al. Study on ductile fracture of 30CrMnSiNi2A steel considering the effect of stress triaxiality[J]. Explosion and Impact, 2021, 41(3):47-54. (in Chinese) 本文引用 [1]

PDF(23699 KB)

Accesses

Citation

Detail

段落导航

摘要
Abstract
关键词
Key words
引用本文
基金
0 引言
1 变截面弹体高速穿甲实验
1.1 实验准备
图1 变截面弹体结构特征图
图2 变截面弹体结构参数图
表1 3类实验弹体结构参数
图3 实验弹体实物图
图4 发射件示意图
图5 实验靶板系统
图6 实验平台示意图
1.2 实验结果与分析
图7 弹体偏转角示意图
表2 弹体速度统计
图8 弹体侵彻靶板的弹道轨迹图
表3 弹体穿甲过程姿态统计
图9 第2层靶板破坏形貌图
图10 回收弹体及冲塞块图
2 数值模拟仿真
2.1 仿真模型的建立
图11 弹靶有限元模型示意图
图12 网格敏感性验证
表4 30CrMnSiNi2A材料模型参数
表5 Q345E材料模型主要参数
2.2 仿真与实验对比分析
图13 仿真靶板破坏形貌图
图14 仿真与实验弹道轨迹图
图15 速度时程曲线仿真与实验数据对比
图16 偏转角时程曲线仿真与实验数据对比
表6 实验与仿真速度对比
表7 实验与仿真偏转角对比
2.3 弹体斜侵彻两层间隔钢靶过程分析
图17 E型弹体纵向加速度-时程曲线
图18 E型弹体纵向位移-时程曲线
图19 弹体穿靶不同阶段图
2.4 变截面弹体结构特征对弹道特性影响分析
表8 变截面弹体参数
图20 弹体侵彻双层间隔钢靶数值模拟示意图
图21 弹体速度时程曲线图
图22 弹体纵向位移时程曲线图
图23 弹体偏转角时程曲线图
图24 不同截面弹体纵向加速度时程曲线图
图25 弹体穿靶过程示意图
3 结论
参考文献

收稿日期	出版日期
2024-01-08	2025-02-28
录用日期	发布日期
2024-03-26	2024-03-26

模态框（Modal）标题

选择文件类型/文献管理软件名称

选择包含的内容

摘要

Abstract

关键词

Key words

引用本文

基金

0 引言

1 变截面弹体高速穿甲实验

1.1 实验准备

图1 变截面弹体结构特征图

图2 变截面弹体结构参数图

表1 3类实验弹体结构参数

图3 实验弹体实物图

图4 发射件示意图

图5 实验靶板系统

图6 实验平台示意图

1.2 实验结果与分析

图7 弹体偏转角示意图

表2 弹体速度统计

图8 弹体侵彻靶板的弹道轨迹图

表3 弹体穿甲过程姿态统计

图9 第2层靶板破坏形貌图

图10 回收弹体及冲塞块图

2 数值模拟仿真

2.1 仿真模型的建立

图11 弹靶有限元模型示意图

图12 网格敏感性验证

表4 30CrMnSiNi2A材料模型参数

表5 Q345E材料模型主要参数

2.2 仿真与实验对比分析

图13 仿真靶板破坏形貌图

图14 仿真与实验弹道轨迹图

图15 速度时程曲线仿真与实验数据对比

图16 偏转角时程曲线仿真与实验数据对比

表6 实验与仿真速度对比

表7 实验与仿真偏转角对比

2.3 弹体斜侵彻两层间隔钢靶过程分析

图17 E型弹体纵向加速度-时程曲线

图18 E型弹体纵向位移-时程曲线

图19 弹体穿靶不同阶段图

2.4 变截面弹体结构特征对弹道特性影响分析

表8 变截面弹体参数

图20 弹体侵彻双层间隔钢靶数值模拟示意图

图21 弹体速度时程曲线图

图22 弹体纵向位移时程曲线图

图23 弹体偏转角时程曲线图

图24 不同截面弹体纵向加速度时程曲线图

图25 弹体穿靶过程示意图

3 结论

{{custom_sec.title}}

{{custom_sec.title}}

参考文献

{{custom_fnGroup.title_cn}}

脚注