PDF(11282 KB)
远场爆炸冲击波作用下高层建筑上部结构动态响应试验研究
殷文骏, 程帅, 刘文祥, 廖真, 马龙, 赵斌, 张德志
兵工学报 ›› 2024, Vol. 45 ›› Issue (11) : 4039-4051.
PDF(11282 KB)
PDF(11282 KB)
远场爆炸冲击波作用下高层建筑上部结构动态响应试验研究
Experimental Study on Dynamic Response of Upper Structure of High-rise Building under Far-field Explosion Shock Wave Loading
为研究高层建筑上部结构在远场爆炸冲击波整体加载作用下的动态响应规律,设计并制作1:30缩比的整体高层建筑模型,完成野外化爆试验,获取建筑模型迎爆面冲击波压力曲线和不同高度位置处的位移曲线,结合数值模拟的方法判断试验加载状态,并对建筑模型的破坏形态和实测数据进行分析。研究结果表明:在远场爆炸冲击波作用下,高层建筑框架柱破坏模式以受剪破坏为主,框架梁构件以弯曲破坏为主,同时不同构件间的相互作用对破坏模式也有重要的影响;爆心与建筑物夹角θ≤25°时,迎爆面各处冲击波压力参数相同;当建筑结构整体仍处于弹性变形阶段时,各高度位置前期水平位移变化曲线近似重合,运动周期保持一致,后期由于高度不同,位移峰值有一定差别,与高度近似呈线性增长的关系;建筑模型的变形与破坏主要取决于比冲量的大小,冲击波峰值影响较小。
In order to study the dynamic response of the upper structure of high-rise building under the far-field explosion shock waveloading, 1∶30 scaled models of high-rise building are designed for the field explosion experiment. The shock wave pressure curves and the displacement parameters at different heights of the modelsare obtained through experiment, and the experimental loading state is judged by the numerical simulation method. The damage patterns of the models and the measured data are analyzed. The results show that the failure mode of high-rise building frame column is mainly subjected to shear failureand the frame beam is mainly subjected to bending failureunder the effect of far-field explosion shock wave. In addition, the interaction between different components has an important influence on the failure mode. When the angle between the explosion center and the building is less than or equal to 25°, the pressure parameters of shock wave are the same all over the surface.When the whole structure is still in the elastic deformation stage, the change curves of horizontal displacement in the early stage of each height position approximately coincide with each other, and the motion periodsare consistent.The peak values of the displacement are different in the later stage due to the different heights, which are linear with the heights. The deformation and damage of the building mainly depend on the specific impulse, and are little affected by the peak shock wave pressure.
高层建筑 / 远场爆炸 / 爆炸冲击波 / 化爆试验 / 位移响应 {{custom_keyword}} /
high-rise building / far-field explosion / explosive shock wave / chemical explosion test / displacement response {{custom_keyword}} /
表1 缩比模型主要物理量相似系数Table 1 Main physical similarity coefficientsin the scaled model |
| 物理性能 | 物理参数 | 量纲 | 相似系数 | 试验选用 相似系数 |
|---|---|---|---|---|
| 几何性能 | 长度 | L | SL | 1/30 |
| 材料性能 | 弹性模量 | ML-1T-2 | Sσ | 0.25 |
| 质量密度 | ML-3 | Sρ | 0.75 | |
| 应变 | 1 | 1 | 1 | |
| 动力响应 | 周期 | T | ST | 0.0577 |
| 加速度 | LT-2 | Sa | 10 |
表2 模型A破坏形态分析Table 2 Failure pattern analysis of Model A |
| 区域编号 | 方向 | 梁 | 柱 | 板 | 剪力墙 |
|---|---|---|---|---|---|
| Ⅰ | 迎爆面 | 少部分梁构件受弯破坏,混凝土开裂或脱落,破坏构件主要集中于中梁;大部分仍保持完好;毁伤数占迎爆面全部梁构件的比例约为40% | 底部(1~3层)中柱构件在剪力作用下破坏严重,其余部分基本保持完好;毁伤数量占迎爆面全部柱构件的比例约为17% | 部分楼板存在扩张型裂纹,但除第9层外大部分保持完整 | 底部剪力墙体完全破坏或脱落,但随着高度的增加,毁伤程度降低;毁伤数量占迎爆面全部剪力墙构件的比例约为100% |
| 背爆面 | 基本保持完整 | 基本保持完整 | 基本保持完整 | 测点处部分墙体破坏严重 | |
| 侧面 | 基本保持完好,存在少量裂纹 | 基本保持完好 | 基本保持完好 | 底部部分混凝土脱落 | |
| Ⅱ | 迎爆面 | 整体破坏较为严重,部分构件混凝土完全脱落,产生贯穿性裂纹;毁伤数量占迎爆面全部梁构件的比例约为78% | 15~17层柱构件破坏严重,部分构件混凝土完全脱落,钢筋裸露;毁伤数量占迎爆面全部柱构件的比例约为17% | 楼板破坏程度较区域Ⅰ更为严重,中间部分存在明显的隆起现象 | 部分混凝土墙体脱落,较区域Ⅰ毁伤程度减轻;毁伤数量占迎爆面全部剪力墙构件的比例约为95% |
| 背爆面 | 基本保持完整 | 基本保持完整 | 基本保持完整 | 测点处部分墙体破坏严重 | |
| 侧面 | 靠近迎爆面一侧的侧梁破坏较为严重,部分混凝土脱落 | 基本保持完好 | 基本保持完好 | 部分靠近迎爆面一侧的混凝土墙体脱落 | |
| Ⅲ | 迎爆面 | 基本保持完整,部分梁构件存在横向裂纹;毁伤数量占迎爆面全部梁构件的比例约为56% | 毁伤程度较为严重,较多构件存在剪切破坏,部分混凝土脱落,少量柱构件完全摧毁甚至消失;毁伤数量占迎爆面全部柱构件的比例约为43% | 顶部楼板完全隆起,与梁、柱构件脱离,其余部分基本保持完整;顶部结构已完全丧失使用性和安全性要求 | 剪力墙体基本保持完好,少部分区域存在扩张性裂纹;毁伤数量占迎爆面全部剪力墙构件的比例约为67% |
| 背爆面 | 基本保持完整 | 基本保持完整 | 基本保持完整 | 基本保持完整 | |
| 侧面 | 基本保持完好 | 少量柱构件存在部分混凝土脱落,基本保持完好 | 顶部靠近迎爆面一侧存在轻微隆起,基本保持完好 | 基本保持完好 |
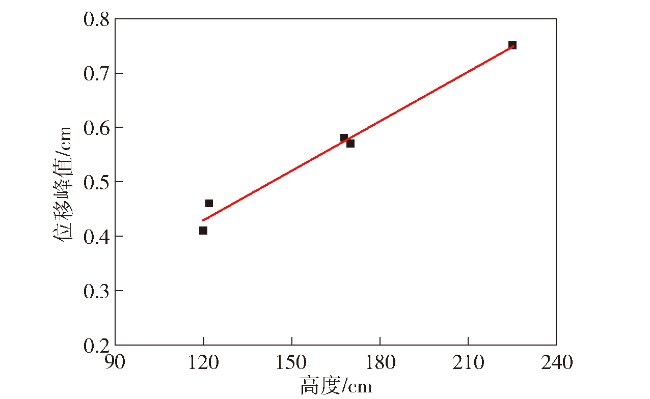
图17 位移峰值随测点高度的变化曲线Fig.17 The curve of displacement peak variation with the height of the measuring point |
表3 模型B位移传感器测点数据Table 3 Displacement data at different measuring points of Model B |
| 参数 | 测点编号 | ||||
|---|---|---|---|---|---|
| D1 | D2 | D3 | D4 | D5 | |
| 坐标/cm | 141120 | 13168 | 138225 | 130170 | 5122 |
| 位移峰值/cm | 0.41 | 0.58 | 0.75 | 0.57 | 0.46 |
| 峰值到时/ms | 26.2 | 28.6 | 35.7 | 30.9 | 26.9 |
表4 两组模型毁伤等级判断Table 4 Damage grade judgment of two models |
| 参数 | 模型A | 模型B |
|---|---|---|
| 爆心距/m | 3.5 | 7.6 |
| 爆炸比距离/ (m·kg-1/3) | 1.75 | 3.80 |
| 物理毁伤描述 | 模型梁、柱、剪力墙等结构件部分发生中度以上破坏,出现局部混凝土脱落、压碎等现象 | 梁、柱、剪力墙基本保持完好,只有顶层各有一根中柱和中梁发生断裂,顶部楼板微微隆起,但未脱离梁柱等结构件 |
| 构件毁伤比例 | 约10%的楼板发生破坏,10%以下的梁、柱构件破坏 | 极少数梁、柱构件破坏,比例小于2% |
| 修复难度 | 承重构件发生破坏,原型需使用大型设备修复 | 承重构件未发生明显破坏,所遭破坏构件均为次要构件,建筑承载力未受影响,无需动用大型设备修复 |
| 功能损伤描述 | 经修复后可继续使用 | 仍可继续使用 |
| 毁伤等级 | 中度 | 轻微 |
| [1] |
《炸药理论》编写组. 炸药理论[M]. 北京: 国防工业出版社,1982.
Compilation Group of “Theory of Explosives”. Theory of explosives[M]. Beijing: National Defense Industry Press, 1982. (in Chinese)
{{custom_citation.content}}
{{custom_citation.annotation}}
|
| [2] |
罗兴柏, 张玉令, 丁玉奎. 爆炸力学理论教程[M]. 北京: 国防工业出版社, 2016.
{{custom_citation.content}}
{{custom_citation.annotation}}
|
| [3] |
{{custom_citation.content}}
{{custom_citation.annotation}}
|
| [4] |
{{custom_citation.content}}
{{custom_citation.annotation}}
|
| [5] |
穆朝民, 任辉启, 李永池, 等. 爆炸冲击波作用于墙体及对墙体绕射的实验研究[J]. 实验力学, 2008, 23(2):169-174.
{{custom_citation.content}}
{{custom_citation.annotation}}
|
| [6] |
{{custom_citation.content}}
{{custom_citation.annotation}}
|
| [7] |
{{custom_citation.content}}
{{custom_citation.annotation}}
|
| [8] |
李月强, 衣娜, 席丰. 钢柱抗爆响应分析单自由度模型适用性评估[J]. 爆炸与冲击, 2017, 37(5):957-963.
{{custom_citation.content}}
{{custom_citation.annotation}}
|
| [9] |
孙松, 王明洋, 邱艳宇, 等. 气爆荷载下弯曲构件动力响应数值计算[J]. 北京理工大学学报, 2019. 39(8):801-807.
{{custom_citation.content}}
{{custom_citation.annotation}}
|
| [10] |
师燕超, 张浩, 李忠献. 钢筋混凝土梁式构件抗爆分析的改进等效单自由度方法[J]. 建筑结构学报, 2019, 40(10): 8-16.
RC beams may be damaged with different failure modes subjected to blast loads. The possible damage modes include flexural failure, direct shear failure, combination of diagonal shear and flexural failure. A dynamic analysis method of structural components under blast loads mainly considers the flexural failure mode and ignores direct shear failure and combination of diagonal shear and flexural failure. Therefore, a quick and accurate blast analysis method for different failure modes is still lacking. In this paper, based on an equivalent single degree of freedom (SDOF) model theory,equivalent SDOF models considering direct shear failure and combination of diagonal shear and flexural failure for RC beams are improved, and the failure criteria and calculation method for the dynamic response of RC beams exhibiting both the direct shear failure and combination of diagonal shear and flexural failure are proposed. Furthermore, considering the combined failure modes, an improved equivalent SDOF method for blast analysis of RC beams is proposed. The procedure for blast analysis of RC beams based on the improved equivalent SDOF method is also presented. The improved method can directly evaluate the failure modes of RC beams under blast loading and calculate structural dynamic responses. Different failure modes and dynamic responses of RC beams under different blast loads are simulated based on software LS-DYNA. The comparison between the simulated results and results calculated from the improved equivalent SDOF method proves that the proposed equivalent SDOF method is valid.
{{custom_citation.content}}
{{custom_citation.annotation}}
|
| [11] |
阎石, 张亮, 王丹. 钢筋混凝土板在爆炸荷载作用下的破坏模式分析[J]. 沈阳建筑大学学报(自然科学版), 2005, 21(3):177-180.
{{custom_citation.content}}
{{custom_citation.annotation}}
|
| [12] |
汪维, 刘瑞朝, 吴飚, 等. 爆炸荷载作用下钢筋混凝土梁毁伤判据研究[J]. 兵工学报, 2016, 37(8):1421-1429.
为研究钢筋混凝土梁在爆炸波作用下的毁伤判据，对两种尺寸的钢筋混凝土梁在缩比条件下进行了不同爆炸距离作用和装药量下的试验研究。试验中以高层和框架结构中最常见的两种 梁为研究对象，通过11次独立的爆炸试验，观测了钢筋混凝土梁在不同装药量下的破坏模式和破坏特征。研究结果表明：钢筋混凝土梁在近区爆炸荷载作用下，在同一爆高下，随着装药量的增加，梁的破坏程度逐渐增加，破坏模式由迎爆面中心两侧少量混凝土脱落和背爆面少量断裂裂纹逐渐增加为迎爆面倒三角锥形式混凝土压碎弯曲破坏，背爆面出现三角锥裂纹和背爆面少量混凝土脱落破坏，最终迎爆面和背爆面三角锥破坏区域贯通形成中心区域压碎崩塌弯曲破坏；崩塌区域的尺寸随着装药量增加而逐渐增加。近区爆炸（以爆距0.5 m为例）作用下，试验钢筋混凝土梁的毁伤判据为：当比例爆高Z>0.4 m/kg<sup>1/3</sup> 时，梁遭受到轻微破坏；当比例爆高0.3 m/kg<sup>1/3</sup>1/3</sup> 时，梁遭受到中等破坏；当比例爆高0.28 m/kg<sup>1/3</sup>1/3</sup>时，混凝土梁遭受重度破坏；当比例爆高Z1/3</sup>，梁遭受严重破坏。在近区爆炸作用下，钢筋混凝土梁的破坏不仅依赖于爆炸比例距离，还与爆高有关，同一比例距离下爆高越大，梁试件的破坏越严重。研究结果可为工程应用及毁伤评估提供参考。
In order to investigate the damage criteria of reinforced concrete (RC) beams under blast loading, the experimental study of two different dimensions of RC beams under different blast distances and charge masses is carried out. Two common RC beams designed for tall buildings and frame structures are taken as the research objects. The damage mode and characteristics of RC beams are got through 11 independent blast experiments. The results show that, when RC beams are subjected to close-in blast loading, the damage level increases with the increase in explosive mass at the same blast distance, the damage mode of RC beams changes from a few fall-off of concrete on the two sides of upper side and a few ruptures on the rear face to the compressed flexural damage of reverse triangle cone-shaped concrete on the upper side and triangle cone-shaped crack and a fall-off of concrete on the rear face, and finally the triangle cone-shaped damage areas on both upper side and rear face are perforated to result in a crushed and punched damage of concrete in the middle area. The damage area increases with the increase in explosive mass. Under close-in blast loading (blast distance= 0.5 m for example), the damage criteria of the RC beams used in the experiment are: the beam suffers from minor damage for scaled burst distance Z>0.4 m/kg<sup>1/3</sup>; it suffers from moderate damage for scaled burst distance 0.3 m/kg<sup>1/3</sup><Z<0.4 m/kg<sup>1/3</sup>; it suffers from high damage for scaled burst distance 0.28 m/kg<sup>1/3</sup><Z<0.3 m/kg<sup>1/3</sup>; it suffers from serious damage for scaled burst distance Z<0.28 m/kg<sup>1/3</sup>. It is also found that the damage of RC beam not only depends on the scaled burst distance under close-in blast loading, but also depends on the burst distance. At the same scaled burst distance, the more the burst distance is, the damage of RC beam is more serious. The results can be useful for engineering application and damage assessments.
{{custom_citation.content}}
{{custom_citation.annotation}}
|
| [13] |
周游, 纪冲, 王雷元, 等. 重复爆炸载荷作用下薄壁方管动力响应研究[J]. 兵工学报, 2019, 40(9):1871-1880.
薄壁方管作为一种典型工程构件，在建筑、海洋、航天等领域应用广泛，其结构面临遭受重复爆炸的风险，开展薄壁方管在重复爆炸载荷作用下的动力响应研究具有重要现实意义。采用实验与数值模拟相结合的方法，对比分析了薄壁方管在单次和重复爆炸载荷作用下的动力响应。将壁厚4 mm、横截面边长100 mm的薄壁方管置于爆炸场中进行冲击实验，并利用非线性动力有限元程序LS-DYNA完全重启动功能及流体与固体耦合算法，对薄壁方管在单次爆炸和重复爆炸载荷下的非线性动力响应过程进行三维数值模拟；描述了方管在不同爆炸次数下的动力响应及损伤变形，给出了一种通过损伤因子反映爆炸载荷作用后材料损伤劣化的数值计算方法。研究结果表明：方管在重复爆炸作用下的变形会产生损伤积累；相同爆炸载荷作用下已变形损伤的方管相对无损方管其有效应变增量更大，在迎爆点周围区域、侧边以及塑性铰位置，前者有效应变增量达到了后者的2.47～3.88倍，容易引起方管更严重的毁伤；两侧边是方管较脆弱的区域，极易因应力集中产生较大的塑性应变，需要特别加强防护。
As a typical engineering component, thin-walled square tube is widely used in construction, ocean and aerospace fields. Its structure may be subjected to the repeated blast loads. It is of practical significance to the research on dynamic response of thin-walled square tube under repeated blast loads. Experimental and numerical investigations were carried out on the dynamic response of thin-walled steel square tubes subjected to single and repeated blasting loads. The impact experiments of thin-walled square tube with 4 mm in wall thickness and 100 mm in cross-section width were made in the explosion field. Based on the full restart function of LS-DYNA and Euler-Lagrange coupling method, the dynamic responses of square tubes subjected to single or repeated blast loads laterally are numerically simulated, and the damage effects under different explosion numbers are described．A numerical method is proposed to reflect the material damage after blast load by damage factor. The results show that the deformation of square tubes subjected to repeated blast loads causes a damage accumulation. Under the same blast load, the deformed square tube has bigger effective strain increment than that of undamaged square tube. In the area around the mid-point, the sides and the plastic hinge position of square tube, the effective strain increment of the former is 2.47-3.88 times of the latter, which may cause the square tube to be damaged more seriously. The two sides of square tube are the weak areas, so it is easy to produce large plastic strain due to stress concentration, and a special protection is needed. Key
{{custom_citation.content}}
{{custom_citation.annotation}}
|
| [14] |
{{custom_citation.content}}
{{custom_citation.annotation}}
|
| [15] |
{{custom_citation.content}}
{{custom_citation.annotation}}
|
| [16] |
{{custom_citation.content}}
{{custom_citation.annotation}}
|
| [17] |
曾繁, 肖桂仲, 冯晓伟, 等. 砌体结构长脉宽爆炸荷载损伤等级评估方法[J]. 爆炸与冲击, 2021, 41(10):127-137.
{{custom_citation.content}}
{{custom_citation.annotation}}
|
| [18] |
{{custom_citation.content}}
{{custom_citation.annotation}}
|
| [19] |
周颖, 吕西林. 建筑结构振动台模型试验方法与技术[M]. 北京: 科学出版社, 2016.
{{custom_citation.content}}
{{custom_citation.annotation}}
|
| [20] |
胡立双, 张清爽, 胡双启. 炸药与火工品安全[M]. 北京: 化学工业出版社, 2021.
{{custom_citation.content}}
{{custom_citation.annotation}}
|
| [21] |
黄正祥, 祖旭东. 终点效应[M]. 北京: 科学出版社, 2014.
{{custom_citation.content}}
{{custom_citation.annotation}}
|
| [22] |
周旭. 导弹毁伤效能试验与评估[M]. 北京: 国防工业出版社, 2014.
{{custom_citation.content}}
{{custom_citation.annotation}}
|
| {{custom_ref.label}} |
{{custom_citation.content}}
{{custom_citation.annotation}}
|
PDF(11282 KB)
文章所在专题
表1 缩比模型主要物理量相似系数
图1 1∶30缩比框架剪力墙模型图2 试验现场布置图3 位移参数测量图4 探针布置图5 探针信号表2 模型A破坏形态分析图6 模型A区域Ⅰ迎爆面图7 模型A区域Ⅱ迎爆面图8 模型A区域Ⅲ迎爆面图9 模型A侧爆面图10 试验后模型B最终破坏形态图11 测点压力时程曲线图12 压力分布数值计算模型图13 建筑模型表面压力场分布计算结果图14 爆心与建筑物夹角图15 θ=19°表面压力场分布计算结果图16 模型B实测位移时程曲线图17 位移峰值随测点高度的变化曲线表3 模型B位移传感器测点数据表4 两组模型毁伤等级判断/
| 〈 |
|
〉 |
