一种刚柔混合弦向变弯度机翼后缘设计

辛涛;李斌

兵工学报 ›› 2023, Vol. 44 ›› Issue (8) : 2465-2476.

EN 投稿 期刊 文章 图表 检索
高级检索

  • 主管：中国科学技术协会

    主编：许毅达

    ISSN 1000-1093

    　

  • 主办：中国兵工学会

    出版：《兵工学报》 编辑部

    CN 11-2176/TJ

《兵工学报》是我国国防科技领域最具影响力的学术期刊之一，创刊于1979年，目前被国内所有重要数据库收录，其综合评价指标近年来一直名列兵工技术类科技期刊的首位；《兵工学报》目前还被国际上著名的检索机构美国......
兵工学报 ›› 2023, Vol. 44 ›› Issue (8) : 2465-2476. DOI: 10.12382/bgxb.2022.0301

一种刚柔混合弦向变弯度机翼后缘设计

作者信息 +

Design of Trailing Edge of a Rigid-flexible Chord-Wise Variable Camber Wing

Author information +
本文二维码
文章历史 +

摘要

为实现机翼在驱动控制下实现弦向连续弯度变化,同时考虑材料变形能力,提出一种刚柔混合式变后缘翼型。通过对翼型中弧线进行几何分析,建立变弯度构型参数化模型,并以升阻比为优化目标,计算最优的刚性段下弯角度以及柔性段下弯曲线。利用计算流体力学计算,对比不同攻角下,刚柔混合偏转翼型和传统刚性偏转翼型的升力系数、升阻比等气动特性。以巡航时单位展长所要求升力为优化目标,分别求解低速巡航及降落两种工况下,两种不同后缘翼型的下弯角度及变形方式。对比两种下偏方式的压力分布、速度分布、气流分离位置等流场特性。根据优化构型制造刚柔混合式变后缘机翼模型,并进行变形能力测试。计算结果表明:刚柔混合后缘翼型在同等偏角下,具有更高的升力系数、升阻比,更优的气动特性;而在相同的飞行工况下,刚柔混合后缘翼型下偏角度要求更小,气流分离点更靠后,具有更高的气动效率。通过变形能力试验验证了柔性翼肋结构及蒙皮设计的合理性。

Abstract

In order to realize the continuously chord-wise camber change of a wing under driving control, with material deformation ability considered,, an airfoil with hybrid (rigid-flexible) variable trailing edge is proposed. Through the geometric analysis of the mean camber line of the trailing edge, the parametric model of variable camber configuration is established. Taking lift-drag ratio as the optimization objective, the optimal bending angle of the rigid section and the optimal curve of the flexible section are calculated. The lift coefficient, lift-drag ratio and other aerodynamic characteristics of the rigid-flexible airfoil and traditional rigid airfoil are compared at different angles of attack by CFD calculation. When the lift required by the unit span during cruise is taken as the optimization objective, the bending angles and deformation modes of two different trailing edge airfoils are solved respectively in low-speed cruise condition and landing condition. The pressure distribution, velocity distribution and separation position of the two bending forms are compared. A wing model with rigid-flexible variable trailing edge based on the optimized configuration is fabricated and the deformation capability testing is conducted. The results show that: the rigid-flexible trailing edge airfoil has higher lift coefficient, lift-drag ratio and better aerodynamic characteristics in same deflection angle; in the same flight condition, the rigid-flexible trailing edge airfoil has a smaller deflection angle and a more backward separation point, so it has a higher aerodynamic efficiency. The rationality of the flexible wing rib structure and skin design has been verified through deformation capability testing.

关键词

弦向变弯度机翼 / 翼型中弧线 / 刚柔混合 / 升阻比 / 变后缘机翼模型

Key words

chord-wise variable camber wing / mean camber line of airfoil / rigid-flexible / lift-drag ratio / variable trailing edge wing model

引用本文

EndNote

Ris (Procite)

Bibtex

导出引用
辛涛 , 李斌. 一种刚柔混合弦向变弯度机翼后缘设计. 兵工学报. 2023, 44(8): 2465-2476 https://doi.org/10.12382/bgxb.2022.0301
XIN Tao , LI Bin. Design of Trailing Edge of a Rigid-flexible Chord-Wise Variable Camber Wing. Acta Armamentarii. 2023, 44(8): 2465-2476 https://doi.org/10.12382/bgxb.2022.0301
中图分类号： V224.5   

基金

国家自然科学基金项目(11872312)

0 引言

变体飞行器在飞行过程中,通过局部或整体改变飞行器的外形形状使飞行器能够实时适应多种任务需求,且使其能够在多种环境下保持最优性能与效率,有效改善飞行器的飞行性能、扩展飞行包线并提高飞行效率[1]。
机翼作为飞机气动力最重要的承载部分,其气动性能直接影响到飞机的性能与飞行效率,因此设计一种外形可根据飞行状态及环境自适应调整的机翼将大幅提高飞机的性能及飞行品质。区别于现代飞机以下放前缘缝翼、后缘襟翼和副翼等增升机构来实现的非光滑连续的翼型弯度变化[2],研制具有连续弦向弯度变化特征的变体机翼是目前变体飞机研究的热点方向之一。对于运输类飞机而言,弦向变弯度机翼一方面可根据飞机实时状态,实时保持最优升阻比,节省燃油,增大航程;另一方面还可以结合控制率的设计,起到飞机载荷减缓、气动弹性剪裁、降噪及结构减重的效益。目前,弦向变弯度机翼的研究主要集中在机翼前缘变弯度以及后缘变弯度技术。
目前,世界各国竞相把弦向变弯度机翼技术作为需要重点研究的技术领域之一。1981年,NASA的Dryden研究所研发 “任务自适应机翼”[3],并在F-111A战斗轰炸机上进行了改装试验。改装后的机翼前后缘各由一部分用玻璃钢制成的活动面组成,可根据不同的飞行条件操纵前后缘的活动面来改变机翼弯度和扭转角。后因机械结构笨重、复杂而未真正应用。自2010年起,NASA与波音公司合作开展了“连续变弯度后缘襟翼系统”项目[4],致力于发展一种新型的采用记忆合金和分布式电机联合驱动的三段式光滑变弯度机翼后缘,该襟翼系统可使飞机在多任务状态下均实现最优升阻比,节省燃油消耗,但该系统目前仍处于原理样机研制阶段。Lu等[5]、Miller等[6]和Kota等[7]利用柔顺机构完成了自适应后缘襟翼设计,并通过试验机上的动态飞行试验,对自适应后缘襟翼在飞行过程中的弯度变化能力进行测试。近年来,NASA利用元胞阵列结构思想,设计制造了结构超轻但同时具备合适刚度及强度的元胞阵列式组合变弯度机翼[8]。Sinapius等[9]提出了“手指”型变形概念,基于传统的机械结构方案,通过内部四连杆设计,实现单自由度驱动。Woods等[10]提出鱼骨方案,基于仿生学原理,实现变弯度设计。Fisher[11]设计制造了一种零泊松比的结构,将鱼骨骨架、蒙皮内部蜂窝结构通过3D打印技术整体制造出来,解决了柔性蒙皮与骨架无法变形匹配的问题。欧洲“洁净天空”项目[12]为支线客机开发了3种变形结构:下垂机头、多功能襟翼和自适应小翼,旨在飞机可根据飞行条件实时调整外形,以达到最优气动效率,并在层流机翼上评估了3种变形装置的效能。Snow等[13]制造了一款柔性机翼,整个机翼为整体结构,不可拆卸,采用3D打印技术制作,讨论了该机翼的性能和稳定性,并提出了展望。Sofla等[14]研究了利用单向形状记忆合金两个非驱动维持的变形位置进行机翼下弯驱动的方法。Yang等[15]利用形状记忆合金作为驱动器对小型无人机的变弯度机翼进行驱动,并进行了该驱动方式下机翼气动性能和气动弹性分析。Vos等[16]描述了如何在可变形机翼结构中使用压电驱动器操纵弯度分布,实现在小型无人机上进行滚转控制。Mkhoyan等[17]设计开发了一种自主变形机翼,提出了一种新的分布式变形概念,这种机翼可以控制机翼展向的升力分布以保证机翼性能达到最优。Jenett等[18]设计了一种基于离散模块化单元的变形机翼,该机翼由离散的单元构成,可以进行连续横向扭转变形,提升了机翼的滚转效率。Zhang等[19]建立了弯度变形机翼气动弹性模型,利用其弦向尺寸和柔性研究了颤振临界速度。通过对比准稳态气动模型和非稳态气动模型,确定准稳态模型对颤振速度的预测更为保守。
国内研究中,杨超等[20]在主动气动弹性机翼及气弹响应载荷减缓方面开战了预先研究。南京航空航天大学研制的基于超声电机驱动的变体机翼采用分布式超声电机驱动刚性后院可转动杠杆,实现机翼弦向变形[21]。张音旋等 [22]设计了一种柔性蒙皮结构,它由柔性蜂窝和弹性胶膜组成,在面内具有较好的变形能力,面外具有一定的承载能力。杨智春等 [23]将多片式翼肋通过连杆滑块及滑动铰组进行连接,设计了可变弯度的机翼后缘结构,同时对其偏转构型、受控运动学规律以及气动特性展开系统性研究。Chen等[24]和冷劲松等[25]基于形状记忆合金与气动肌腱展开弦向变弯度机翼结构设计研究。陈秀等[26]提出基于连续拓扑优化方法的全柔性机翼结构设计方案,将拓扑优化方法与机翼结构设计相结合,并分别对机翼的前后缘变弯度结构进行了优化设计研究。徐钧恒等[27]提出一种基于交叉簧片铰链的变弯度机翼,建立了其力学模型并对其进行了优化设计,试验结果表明该机翼具有较大的变形能力,并能实现机翼连续弦向变弯度。王宇等[28]采用零泊松比蜂窝结构柔性材料做柔性蒙皮,设计了一种弯梁和平面盘带动后缘偏转的结构,并研究了其多学科设计与优化方法。尉濡恺等[29]开展了基于变弯度后缘的阵风响应减缓数值研究,研究发现相比于传统铰链舵面,变弯度后缘在阵风减缓控制方面具有更大的潜力。
对比近年来变弯度机翼相关工作,形状记忆合金、压电陶瓷、超声电机等新型驱动技术成为国内外学者关注的热点。其中,形状记忆合金具有大应变、大应力的优点,但金属丝加热和冷却所需时间较长,驱动能力受环境因素影响较大,驱动性能不稳定、效率低下;同时,金属丝的疲劳寿命会严重制约驱动器的使用时间。压电材料虽然具有灵敏度高、可设计性强等优点,但其驱动速度较慢,同时可输出的变形量有限,更适用于小型变体飞行器。超声电机具有体积小、可控性强优点,但往往由于其体积较小,因此输出驱动力较小,并且在使用时需要多电机驱动,增加结构重量,会降低柔顺结构带来的气动效益。
柔顺机构是一种将输入载荷通过自身弹性变形实现输出端位移变化,并以应变能的形式储存部分输入能量的机构。通过柔顺机构可自然使结构在目标方向实现连续光滑的变形,同时减少结构所需的零部件数目,取代传统机械传动方式的运动副,使得机构磨损降低,驱动效率提升。
弦向变弯度机翼的设计主要难点分别为结构设计、蒙皮匹配设计以及驱动设计。其中结构设计尤为重要,而在结构设计之初,机翼的弦向变弯度构型尤其重要,决定着变形后机翼是否满足设计要求,气动效率是否达到最优,以及不同偏转工况下材料应力水平是否合理等。
鉴于此,本文将柔顺机构引入弦向变弯度机翼设计中,考虑材料的弹性许可变形能力可兼顾增升指标需求和最优升租特性实现需要,设计了一种刚柔混合偏转的机翼后缘原理样机。首先,综合考虑驱动方式、结构材料、偏转目标角度等因素确定刚柔混合后缘偏转段中刚性及柔性部分的占比;其次,通过翼型的中弧线对其变弯构型进行几何参数化描述;再次,以翼型升阻比作为优化目标,通过遗传算法结合XFOIL软件计算确定最优弯度构型,并通过计算流体力学(CFD)确认优化构型的精确升阻特性,对比了传统刚性偏转后缘与刚柔混合式后缘在不同飞行工况下的升力系数、升阻比、流场特性等;然后,介绍了柔顺段翼肋的结构优化原理和过程,以及滑动蒙皮的设计方法;最后制造和装配了刚柔混合式后缘机翼偏转段,完成了初步的变形能力测试。

1 变弯度构型总体结构分析

安装在机翼后缘的襟翼通常占机翼剖面总弦长的25%~35%。以某中程中型运输机的襟翼系统为设计参考,确定机翼设计总弦长为3.33m,后缘变弯度段为1m,占比为30%,弦向变弯度后缘的目标偏转角度为30°。选用NACA0012翼型为基础参考翼型,进行设计及优化。
变弯度机翼后缘设计中,输入点、结构形式,以及输出点3部分构成基本设计元素。输入点即驱动器的输出位置,其形式可以分为集中式单点驱动与分布式驱动两类驱动方法。结构形式通过拓扑、尺寸、形状等优化方法得到。弦向变弯度后缘输出点集即为翼肋结构的外轮廓线。本文重点聚焦刚柔混合变弯度后缘的气动特性优化、可变形翼肋的刚柔组合设计及原理可行性验证。暂不涉及对忽略弦长变化、蒙皮匹配、及承载能力验证。
本文选用航空7075-T6硬铝合金为可变体翼肋的设计材料。通过有限元分析可知,若将整个后缘变形段均设计为柔顺结构,则当结构下弯至目标角度时,其上下翼缘应力会超出材料的许用应力。进一步分析翼型后缘中弧线的连续变弯度需求可知,机翼后缘变形与悬臂梁受载下弯变形类似,悬臂梁型[19]后缘变形中弧线变形初始段和翼尖段呈现类似等斜率分布。因此综合考虑翼肋材料的弹性许可变形能力,兼顾增升指标需求和最优升租特性实现需要,本文提出如图1所示的刚柔混合可变形翼肋设计方案。在机翼后缘变弯度段按照刚性、柔性与随动三段交替布置结构类型,分别占整个机翼后缘的30%、40%以及30%。
图1 翼肋后缘结构布局示意图

Fig.1 Structure layout of wing rib trailing edge

Full size|PPT slide

2 翼型变弯度构型的参数化描述与优化设计

对于柔性机翼后缘而言,若固定变弯度段的目标偏转角度,如30°,实际实现这一偏转目标的偏转曲线构型有多种选择,中弧线两点之间可以由不同曲线构成。因此需基于机翼气动性能确定最优的翼型变弯度构型,使其刚柔连接处具有较好的连续性,且整体具有最优的升阻比特性。
将变弯度构型后缘划分为刚性偏转段、柔性段和随动段,并利用中弧线对其几何特征进行描述,把相对复杂的翼型参数化问题简化成了曲线参数化问题。为确保弯度变化连续性与光滑性,同时增加弯度变化描述的多样性,采用三次样条线方程来描述翼型中弧线:
y=a1x3+a2x2+a3x+a4∫xsxe1+dydx2dx=lys=0ye-ys=(xe-xs)·tan(θ2)
(1)
式中:a1~a4为三次样条线方程的系数;(xs,ys)为中弧线初始偏转点坐标;(xe,ye)为中弧线尾缘点坐标;l为变弯度后缘段中弧线长度;θ2为变弯度后缘段等效偏转角。
刚柔混合结构形式下翼型中弧线如图2所示。
图2 翼型后缘中弧线

Fig.2 Mean camber line of trailing edge of airfoil

Full size|PPT slide

图2中,m0~m5这6个点均位于翼型中弧线上,其中m0为机翼变弯度段的初始点,令其为坐标原点,θ1为刚性偏转角。m5为后缘点,m1、m4分别为刚柔结合处的结合点,为保证刚性段与柔性段的光滑连续,柔性段方程在m1点坐标处的切线方向应与刚性转动段的斜率保持一致,柔性段 m2、m3分别为横坐标为400mm以及600mm且位于柔性段中弧线上的点,将各点坐标代入式(1),可得
xm0=ym0=0ym1=xm1·tan(θ1)f'(x)|x=xm1=3a·xm12+2b·xm1+c=tan(θ1)ym1=a·xm13+b·xm12+c·xm1+dym2=a·xm23+b·xm22+c·xm2+dym3=a·xm33+b·xm32+c·xm3+dym4=a·xm43+b·xm42+c·xm4+dym5-ym4xm5-xm4=f'(x)|x=xm4=3a·xm42+2b·xm4+c∫xm1xm41+(3a·x2+2b·x+c)2dx=lm1m4(ym5-ym4)2+(xm5-xm4)2=lm4m5
(2)
式中:( xmi, ymi)为mi点的坐标,i=0,1, …,5;a、b、c、d为系数; lm1m4为m1点和m4点间的弧长; lm4m5为m4点和m5点间的弧长。
通过对式(2)中各式的联立化简,可将中弧线曲线各参数化为关于刚性偏转角θ1以及点m2的y坐标的方程,因此以刚性偏转角θ1及点m2的y坐标绝对值为优化问题的设计变量。由于弦向变弯度翼型其优势在于相较传统翼型升阻特性的提升,因此最优变弯度构型的评价函数S为翼型的最大升阻比:
S=max (CL/CD)
(3)
式中:CL为升力系数;CD为阻力系数。
通过利用遗传算法,计算相应变弯度构型的升阻比。机翼后缘目标下偏角30°为设计最大偏转角,对应于飞机的降落(最大偏转角)状态,所以流场参数设置为飞机降落工况,如表1所示。
表1 翼型状态及环境参数

Table 1 Airfoil state and operating parameters

攻角/
(°)		 马赫数 空气密度/
(kg·m3)		 空气动力黏度/
(Pa·s)		 雷诺数
8 0.2 1.205 1.78938×10-5 4.58×106
计算流程如图3所示。
图3 最优翼型优化流程图

Fig.3 Optimization process of optimal airfoil

Full size|PPT slide

优化过程设定如下约束条件:考虑材料强度限制,柔顺段与随动段产生的最大许可等效弦向弯度偏转角为15°。对应该约束条件,根据式(3)中评价函数计算最终得到最优结果为θ1=20.06°、 ym2=-163.87。对中弧线坐标进行归一化后,绘制该中弧线对应的翼型轮廓线,得到最终变弯度构型如图4所示。
图4 柔顺翼肋最优变弯度构型

Fig.4 Optimal configuration of flexible rib

Full size|PPT slide

并将优化得到的刚柔混合可变性翼肋中弧线及翼型轮廓线与悬臂梁型后缘变形中弧线及翼肋进行对比,如图5所示。变弯度后缘翼型轮廓线差异最大仅为翼型弦长的1.1%,是后缘变弯度特征弦长的3.5%。
图5 刚柔混合型与悬臂梁型变弯度构型对比

Fig.5 Comparison of hybrid rib and cantilever rib

Full size|PPT slide

3 气动特性分析

基于优化得到刚柔混合变后缘翼型及传统刚性偏转翼型,通过计算流体力学分析,对比分析其流场特性及气动力特性。
以刚柔混合可变弯度后缘翼型偏转30°为例,其网格模型如图6所示。
图6 计算网格

Fig.6 Computational grid

Full size|PPT slide

计算采用k-ω SST湍流模型,流体介质为理想气体,温度为300K,参考标准大气压为101325Pa,马赫数为0.2,参考弦长为1000mm。
图7为后缘偏转角度30°时,两种不同偏转方式升力系数随攻角变化曲线。由图7可以看出,在相同的后缘偏角下,刚柔混合偏转方式的升力系数始终比刚性偏转后缘翼型的升力系数大,且在负攻角时更为突出。当攻角为-4°时,刚柔混合偏转翼型升力系数是传统刚性偏转翼型的1.66倍,当攻角为8°时,刚柔混合偏转翼型升力系数是传统刚性偏转翼型的1.12倍。其原因是刚柔耦合偏转方式的压力分布在后缘部分更光滑连续,其围成的面积始终较大,增升效果更加明显。
图7 升力系数对比

Fig.7 Comparison of lift coefficient

Full size|PPT slide

图8为后缘偏转角度30°时,两种不同偏转方式升阻比随攻角变化曲线。由图8可以看出,在相同的后缘偏角下,刚柔混合偏转后缘翼型的升阻比始终较刚性偏转后缘翼型大,但随着攻角增加,刚柔混合偏转翼型的升阻比优势会有所减弱。当攻角为-4°时,刚柔混合偏转翼型升阻比是传统刚性偏转翼型的2.86倍,当攻角为8°时,刚柔混合偏转翼型升阻比是传统刚性偏转翼型的1.37倍。对比文献[30]中SM_3构型,该翼型设定在弦长70%~90%处实现柔性下弯变形,通过计算,刚柔混合变弯度翼型与该构型得到的升力特性与升阻比特性表现出相似结果。
图8 升阻比系数对比

Fig.8 Comparison of CL/CD coefficients

Full size|PPT slide

为了更全面验证刚柔混合偏转翼型的升阻特性优势,结合运输机实际飞行工况,以飞机正常巡航时单位展长机翼的升力为目标,分别优化计算低速巡航工况及降落工况下两种偏转形式达到目标升力时的偏转构型如表2所示,并使用CFD进行验证。
表2 刚柔混合翼型后缘偏转构型

Table 2 Configuration of rigid-flexible trailing edge of airfoil

飞行工况 攻角/
(°)		 马赫数 高度/
m		 刚性偏
角/(°)		 柔性偏
角/(°)
低速巡航 4 0.35 100 0 8.7
降落工况 8 0.2 0 3.78 15
由表2可知,当飞行工况为低速巡航时,刚柔混合翼型不需刚性偏转,仅驱动占翼型弦长21%的柔性段及随动段,使其达到等效下偏角8.7°即可获得目标升力,而传统刚性偏转翼型则需要将占翼型弦长30%的整体后缘偏转7.3°才能达到目标升力。当飞行工况为降落工况,该工况普遍对应机翼后缘下弯最大的情况,刚柔混合翼型仅需刚性偏转3.78°,柔性偏转15°,后缘整体等效下弯16.05°,便可达到目标升力,而传统刚性偏转翼型则需整体下弯29°,才可达到目标升力。
对上述两种翼型在不同工况下进行CFD仿真验证。对于飞行工况为低速巡航状态,达到同等升力要求时,传统刚性偏转翼型整体后缘偏转角度为7.3°,其升阻比为43.78,而刚柔混合偏转翼型,仅需驱动占翼型弦长21%的柔性机翼下偏8.7°即可达到同等效果,且此时升阻比为45.53,较传统刚性偏转增加3.9%,从而大幅提高运输飞机的经济性[31]。可见刚柔混合柔顺变后缘机翼方案提供了一种新的增升装置设计思路,短弦长的柔顺下弯在保持相同的增升效应时,可有效提升升阻比[32]。
由图9及图10可以看出,在低速巡航工况下,两种偏转方式具有类似的压力分布、速度分布及流场特性,由于攻角及后缘偏转角度较小,在翼型尾部均未出现严重的气流分离。
图9 低速巡航工况压力云图对比

Fig.9 Comparison of pressure nephograms of low-speed cruise

Full size|PPT slide

图10 低速巡航工况速度云图及流线对比

Fig.10 Comparison of velocity nephogram and streamline of low-speed cruise

Full size|PPT slide

对于飞行工况为降落状态,达到目标升力时,传统刚性偏转翼型整体后缘偏转角29°,其升阻比为9.03,而刚柔混合偏转对应翼型后缘整体等效下弯角度仅为16.05°,其升阻比为16.11,较传统刚性偏转增加78.41%。可以看出,该偏转形式大大改善了翼型后缘偏转时的连续性与光滑性,使其具有更优的升阻特性。在大角度下弯时,其升阻比优势更为明显。
图11为降落状态下两种构型对应的压力分布云图,对比图11(a)与图10(b)可知,刚柔混合偏转翼型在尾部形成的低压区面积明显小于传统刚性偏转翼型。图12为该工况下两种构型对应的速度云图及流线图,可以看到图12(a)中刚柔混合偏转翼型尾缘处的气流分离起始位置位于x/C=0.8处,C为弦长,图12(b)中传统刚性偏转翼型尾缘处的气流分离起始位置位于x/C=0.57处。且对比两图,图12(b)中翼型尾缘处气流分离形成的涡结构尺度明显大于图12(a)中翼型,可见,传统刚性偏转翼型会过早的出现气流分离,严重影响气动效率,而刚柔混合偏转翼型更不易产生气流分离,其分离点更靠近尾缘,气动效率更佳。图13为降落工况下两种构型对应的翼型上下表面压力分布,对比图13(a)与图13(b)可以明显看出,刚柔混合偏转翼型在其偏转处具有更好的连续性与光滑性,突变效应更小。
图11 降落工况压力云图对比

Fig.11 Comparison of pressure nephogram of landing

Full size|PPT slide

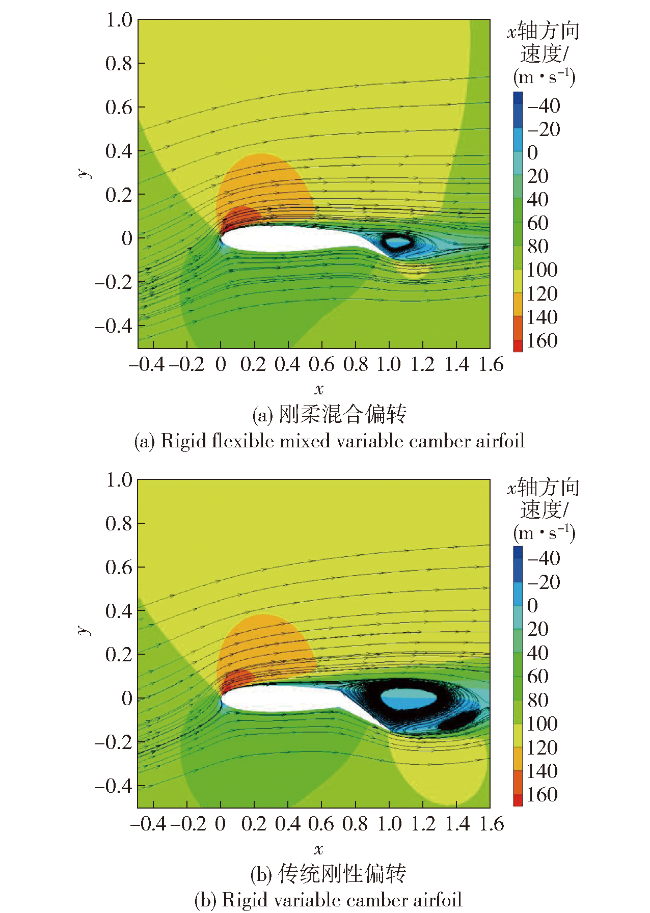
图12 降落工况速度云图及流线对比

Fig.12 Comparison of velocity nephogram and streamline of landing

Full size|PPT slide

图13 降落工况翼型上下表面压力系数对比

Fig.13 Comparison of pressure coefficients of upper and lower surfaces of airfoil

Full size|PPT slide

4 变形能力试验研究

确定最优变弯度构型的气动设计方案,变后缘机翼设计重要工作是实现刚柔混合机翼的结构和变形控制设计[33]。本文在此略去具体的刚柔混合机翼优化设计过程,仅简要描述设计原理和结果。设计的关键在于柔顺翼肋的设计,该翼肋结构设计时采用载荷路径法进行拓扑优化,如图14所示。载荷路径法在初始布局时与基结构优化方法类似,通过载荷路径的传递形式将设计域内的特征点进行连接,通过中间点的位置及数量,控制拓扑解的多样性。首先在设计域中布置适当的节点数量,通过满基构型给出设计域初始的拓扑结构形式;之后通过将载荷路径参数化、离散化,形成载荷输入点至输出点的不同路径形式;然后采用合适的设计变量,如路径编号、路径权值等,通过优化算法结合有限元分析得到限制条件下载荷输入点到载荷输出各点的最优路径,最终将涵盖这些路径的所有结构进行组合,便得到了最终的拓扑优化结果。
图14 基于载荷路径法的拓扑优化流程

Fig.14 Topology optimization process based on load path method

Full size|PPT slide

图15中:点1为驱动载荷的输入点;点1~点6分别为上、下翼缘面上的输出点;点7~点11为设计域中间节点;点12为固定点。首先利用计算机图论中Dijkstra贪心算法求解输入点至各输出点的最短路径,再利用 YEN算法,通过解得的最短路径求解输入点至输出各点的前K条载荷传递路径。当 K=4时,所有路径均已涵盖所有初始基结构。
图15 柔顺段拓扑优化设计区域示意图

Fig.15 Schematic diagram of topology optimization design area of flexible section

Full size|PPT slide

根据不同路径,通过有限元分析设计域中每根梁结构在某条路径中是否被调用,如果调用则其在有限元模型中保留,如未被使用,则有限元模型中对该梁进行删除。同时对结构尺寸及形状进行交替优化[34],并引入稳定性及变形能力更为出色的变截面曲梁代替原等截面直梁,以柔顺段结构在驱动力作用下的变弯度构型与之前得到的最优变弯度构型的贴合程度为评价标准,建立其实际变弯度构型与目标构型的最小二次方差作为该空间优化过程的目标函数:
min f(x)=∑i=1n(xi-x¯i)2+(yi-y¯i)2
(4)
得到了目标变形要求下符合材料强度要求的最优结构构型,如图16所示。
图16 刚柔混合后缘结构

Fig.16 Rigid-flexible trailing edge structure

Full size|PPT slide

为提高变弯度后缘的承载能力,以真实气动载荷为技术指标来对变弯度后缘进行进一步优化设计。以降落时柔顺段下弯15°为分析工况,计算单位展长内真实气动载荷,其上下翼面压力系数如图17所示。经机翼传力特性分析,需在单位展长内进行5根翼肋布置,且需将单根翼肋延展向厚度增至 20mm, 可达到承载所需的刚度与结构强度。式(5)为翼肋上、下缘气动载荷延弦向分布:
图17 刚柔混合变弯度翼型压力系数

Fig.17 Pressure coefficient of rigid-flexible variable camber airfoil

Full size|PPT slide

ydown=-2464x3+1.414×104x2-2.599×104x+　　3.636×104yup=390.9x3-3380x2+9746x+1.02×104
(5)
式中:x为延弦向位置;y为对应的气动载荷。由于结构刚度的增加,需将单根气动肌腱驱动力提升至3250N,便可实现预期的结构变形。本文仅对结构变弯度能力进行验证,故暂不考虑气动载荷影响。
蒙皮设计中,刚性转动段根据机翼表面在变形过程中保持光滑连续的要求,设计了抽拉式蒙皮结构,如图18所示,上下翼面蒙皮分别沿设置的蒙皮滑动轨道伸入翼盒前缘,通过固定在前缘翼梁上的弹簧连接。当机翼刚性转动段向下偏转时,此处上翼面蒙皮会沿轨道拉出,此时拉力弹簧处于拉伸状态,通过弹簧恢复力张紧蒙皮,下翼面蒙皮在初始位置时已进行弹簧预拉伸,沿轨道插入翼盒内部后,弹簧扔就保持拉伸状态,为蒙皮提供了一定的面外刚度。抽拉式蒙皮设计使机翼结构在前后缘蒙皮间隔处保持了相对的光滑性和连续性。在柔性段处,目前上下翼面均采用滑动蒙皮设计,通过张紧的滑动钢索及滑块导轨装置连接蒙皮与翼肋结构,保证了连接处的柔顺特性,使其可随翼肋同时变形。由于上下蒙皮在翼肋末端处非封严结构,可能对气动效率及蒙皮结构的强度造成影响,因此,通过分析翼肋末端处上下蒙皮的运动轨迹,设计并通过3D打印技术制造了蒙皮连接加强结构,如图19所示,将其固定于上下蒙皮之间,使得变形过程中,翼肋末端处上下蒙皮始终紧密贴合。
图18 刚性段抽拉式蒙皮设计

Fig.18 Skin in pull mode in rigid section

Full size|PPT slide

图19 翼肋末端处上下翼面连接结构

Fig.19 Connecting structure of upper and lower wing surfaces at the end of wing rib

Full size|PPT slide

对优化得到的翼肋结构进行加工制造,选用材料为7075-T6航空硬铝合金。刚性转动段采用伺服电机及曲柄连杆机构驱动,通过作动输出端的水平运动转化为翼肋结构的定轴转动,柔性变形段中每个翼肋采用两根气动肌腱共同驱动,通过电压控制气动肌腱进气量,从而改变其内部压强,最终将气动肌腱的轴向变形转换为驱动力输出[35-36]。进行装配后,得到了3翼肋翼盒模型,如图20所示。
图20 刚柔混合变后缘模型

Fig.20 Rigid-flexible variable trailing edge model

Full size|PPT slide

以最大等效下偏角30°进行所设计变体机翼后缘的变形验证试验。3翼肋翼盒结构在伺服电机驱动下,首先进行刚性偏转,其转动角度与驱动器水平作动距离可由其几何关系直接计算得到,当刚性转动段下弯20°时,伺服电机驱动的水平位移为 21mm。 当刚性转动段旋转至指定位置时,对伺服电机驱动器进行锁死。在此基础之上,维持刚性转动不变,应用气动肌腱进行柔顺段的下弯驱动。试验结果表明,给气动肌腱施加3.9bar压力(6.5V气动阀驱动电压),则可实现柔顺段结构等效偏转角度达到15°、整体后缘达到下弯30°的目标,如图21所示。
图21 不同驱动下后缘变形形态

Fig.21 Deformation shape of trailing edge under different driving conditions

Full size|PPT slide

5 结论

本文综合考虑可变幅度、变形连续性、变形应力及驱动效率等因素,提出一种刚柔混合偏转翼型设计方案,并与传统偏转方式进行了气动效率对比,然后根据实际气动载荷给出了翼肋结构及驱动器布置方案,最后通过试验验证了刚柔混合变弯度后缘机翼结构及蒙皮的变形能力。
首先建立了以翼型中弧线为基础的机翼变弯度构型参数化几何描述方法,对应后缘30°的偏转目标,以翼型升阻比为评价函数,最终优化得到了刚、柔两部分最优的下偏角度以及柔性部分变弯度曲线,从而得到最优的变弯度构型。
其次通过CFD仿真对比了后缘下偏30°构型,两种翼型在不同的攻角下的升力系数、升阻比等气动特性。结果表明,在-4°~8°攻角下,刚柔混合翼型的升力系数、升阻比均优于传统刚性偏转翼型,且在小攻角较为明显,原因是攻角增大后,尾部出现气流分离导致阻力上升,气动效率下降。
然后对照飞机实际飞行工况,以单位展长内机翼升力作为优化目标,分别计算了两种偏转形式翼型在低速巡航及降落工况下的最优下偏角度。在低速巡航工况下,为提供目标升力,刚柔混合式偏转机翼只需驱动柔性段下偏8.7°即可满足要求,而传统刚性偏转机翼需将整个后缘段下偏7.3°。在降落工况下,刚柔混合式偏转机翼需将刚性段偏转3.78°,柔性段偏转15°,总体等效偏转16.1°即可达到优化目标,而传统刚性偏转机翼需将整个后缘段下偏29°才可满足。更进一步地,利用CFD仿真进行了流场特性计算,发现:在大偏角情况下刚柔混合偏转翼型的优势更大,降落工况中,其升阻比较传统刚性偏转翼型增加78%;气流分离点位置更靠近翼型后缘,仅为x/c=0.8处,且后缘处的涡结构更小,气动效率更高。
通过实际气动载荷计算,给出了上下翼面延弦向的压力分布,并通过有限元分析确定了翼肋展向厚度及单位展长内布置的翼肋数量。由于单根柔顺段翼肋结构重量仅为0.35kg,且气动肌腱及控制模快质量均远低于传统液压驱动装置,因此在结构减重方面也有较大的优势。
最后介绍了柔顺翼肋结构优化的原理及方法,以及刚性转动段和柔顺段的蒙皮设计方法,并进行了模型制造及不考虑气动载荷情况下的变形能力试验,通过伺服电机及气动肌腱分别对刚柔混合偏转后缘的刚性段及柔性段进行驱动,在刚性段下弯至20°后,气动肌腱驱动电压达到6.5V时,刚柔混合下弯角度达到设计值30°,同时记录了不同电压下的变形状态。

参考文献

原文顺序 | 文献年度倒序 | 文中引用次数倒序
[1]
刘卫东. 变形机翼关键技术的研究[D]. 南京: 南京航空航天大学, 2014.
LIU W D. Research on key technology of morphing wing[D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2014. (in Chinese)
本文引用 [1]
[2]
王彬文, 杨宇, 钱战森, 等. 机翼变弯度技术研究进展[J]. 航空学报, 2022, 43(1):144-163.
WANG B W, YANG Y, QIAN Z S, et al. Technical development of variable camber wing: review[J]. Acta Aeronautica et Astronautica Sinica, 2022, 43(1): 144-163. (in Chinese)
本文引用 [1]
[3]
DECAMP R W, HARDY R. Mission adaptive wing research programme[J]. Aircraft Engineering and Aerospace Technology, 1981, 53(1): 10-11.
本文引用 [1]
[4]
UMES J, NGUYEN N. A mission adaptive variable camber flap control system to optimize high lift and cruise lift to drag ratios of future N+3 transport aircraft[C]// Proceedings of AIAA Aerospace Sciences Meeting Including the New Horizons Forum and Aerospace Exposition. Grapevine, TX, US: AIAA, 2013.
本文引用 [1]
[5]
LU K J, KOTA S. Parameterization strategy for optimization of shape morphing compliant mechanisms using load path representation[C]// Proceedings of ASME 2003 International Design Engineering Technical Conferences and Computers and Information in Engineering Conference. Chicago, IL, US: ASME, 2003:693-702.
本文引用 [1]
[6]
MILLER E J, CRUZ J, KOTA S, et al. Evaluation of the hinge moment and normal force aerodynamic loads from a seamless adaptive compliant trailing edge flap in flight[C]// Proceedings of the 54th AIAA Aerospace Sciences Meeting. San Diego, CA, US:AIAA, 2016:2016-0038.
本文引用 [1]
[7]
KOTA S, FLICK P, COLLIER F S. Flight testing of flex Floil TM adaptive compliant trailing edge[C]// Proceedings of the 54th AIAA Aerospace Sciences Meeting. San Diego, CA, US: AIAA, 2016:2016-0036.
本文引用 [1]
[8]
CRAMER N B, CELLUCCI D W, FORMOSO O B, et al. Elastic shape morphing of ultralight structures by programmable assembly[J]. Smart Materials and Structures, 2019, 28(5):055006.
https://doi.org/10.1088/1361-665X/ab0ea2
https://iopscience.iop.org/article/10.1088/1361-665X/ab0ea2
本文引用 [1]
[9]
SINAPIUS M, MONNER H P, KINTSCHER M, et al. DLR’s morphing wing activities within the European network[J]. Procedia Iutam, 2014, 10: 416-426.
https://doi.org/10.1016/j.piutam.2014.01.036
https://linkinghub.elsevier.com/retrieve/pii/S2210983814000376
本文引用 [1]
[10]
WOODS B K S, FRISWELL M I. Preliminary investigation of a fishbone active camber concept[C]// Proceedings of ASME 2012 conference on Smart Materials, Adaptive Structures and Intelligent Systems. Stone Mountain, GA, US: ASME, 2012:555-563.
本文引用 [1]
[11]
FISHER C. Inspired by fish[EB/OL]. [2022-04-01]. https://aerospaceamerica.aiaa.org/department/inspired-by-fish/
https://aerospaceamerica.aiaa.org/department/inspired-by-fish/
本文引用 [1]
[12]
DIMINO I, MOENS F, PECORA R, et al. Morphing wing technologies within the airgreen 2 project[C]// Proceedings of AIAA Scitech 2022 Forum. Reston, VA, US: AIAA, 2022: 0718.
本文引用 [1]
[13]
SNOW S A, HUNSAKER D F. Design and performance of a 3D-printed morphing aircraft[C]// Proceedings of AIAA SciTech 2021 forum. Reston, VA, US: AIAA, 2021: 1060.
本文引用 [1]
[14]
SOFLA A Y N, ELZEY D M, WADLEY H N G. Two-way antagonistic shape actuation based on the one-way shape memory effect[J]. Journal of Intelligent Material Systems and Structures, 2008, 19(9): 1017-1027.
https://doi.org/10.1177/1045389X07083026
http://journals.sagepub.com/doi/10.1177/1045389X07083026
本文引用 [1]
[15]
YANG S M, HAN J H, LEE I. Characteristics of smart composite wing with SMA actuators and optical fiber sensors[J]. International Journal of Applied Electromagnetics and Mechanics, 2006, 23(3/4): 177-186.
https://doi.org/10.3233/JAE-2006-736
https://www.medra.org/servlet/aliasResolver?alias=iospress&doi=10.3233/JAE-2006-736
本文引用 [1]
[16]
VOS R, BARRETT R, DE B R, et al. Post-buckled precompressed elements: a new class of control actuators for morphing wing UAVs[J]. Smart Materials and Structures, 2007, 16(3): 946-957.
本文引用 [1]
[17]
MKHOYAN T, THAKRAR N R, de REUKER B R, et al. Design of a smart morphing wing using integrated and distributed trailing edge camber morphing[C]// Proceedings of ASME 2020 Conference on Smart Materials, Adaptive Structures and Intelligent Systems. Online:ASME, 2020: V001T04A023.
本文引用 [1]
[18]
JENETT B, CALISCH S, CELLUCCI D, et al. Digital morphing wing:active wing shaping concept using composite lattice-based cellular structures[J]. Soft robotics, 2017, 4(1): 33-48.
https://doi.org/10.1089/soro.2016.0032
https://www.liebertpub.com/doi/10.1089/soro.2016.0032
本文引用 [1]
[19]
ZHANG J Y, ALEXANDER D S, CHEN W, et al. Aeroelastic model and analysis of an active camber morphing wing[J]. Aerospace Science and Technology, 2021, 111:16534.
本文引用 [2]
[20]
杨超, 陈桂彬, 邹丛青. 主动气动弹性机翼技术分析[J]. 北京航空航天大学学报, 1999, 25(2):171-175.
YANG C, CHEN G B, ZOU C Q. Analysis of active aeroelastic wing technology[J]. Journal of Beijing University of Aeronautics and Astronautics, 1999, 25(2):171-175. (in Chinese)
本文引用 [1]
[21]
刘卫东, 丁倩, 朱华, 等. 基于超声电机的变弯度翼的驱动与集成[J]. 振动、测试与诊断, 2013, 33(5):856-861.
LIU W D, DING Q, ZHU H, et al. Drive and integration techniques of variable camber wing based on ultrasonic motors[J]. Journal of Vibration, Measurement&Diagnosis, 2013, 33(5):856-861. (in Chinese)
本文引用 [1]
[22]
张音旋, 邱涛, 王健志. 一种柔性蒙皮设计技术及其在后缘变弯度机翼结构中的应用[J]. 航空科学技术, 2012(5):26-28.
ZHANG Y X, QIU T, WANG J Z. A flexible skin design technology and the application on variable camber trailing edge[J]. 2012(5):26-28. (in Chinese)
本文引用 [1]
[23]
杨智春, 解江. 柔性后缘自适应机翼的概念设计[J]. 航空学报, 2009, 30(6): 1028-1034.
摘要
对H.P.Monner提出的 “可转动翼肋”自适应机翼概念进行运动学研究，推导了驱动位移量和偏转变形量之间的对应关系。这种可变形翼肋可简化为由平面连杆机构组合而成的单自由度系统，能使机翼后缘柔性偏转的同时保持翼面光滑连续。提出了基于曲线逼近原理根据后缘中弧线偏转轨迹优化转轴点布局的翼肋机构设计方法。对悬臂梁型、圆弧型和反悬臂梁型3种偏转距离相等但偏转轨迹不同的柔性后缘进行了方案设计和分析，从翼肋机构的实现、承载能力以及气动特性3方面进行了建模计算和比较研究。结果表明，圆弧型是3种柔性后缘中最佳的设计方案；柔性后缘自适应机翼的设计分析方法是切实可行的，可根据实际需要设计出满足任意后缘偏转要求的自适应机翼。
YANG Z C, XIE J. Concept design of adaptive wing with flexible trailing edge[J]. Acta Aeronautica et Astronautica Sinica, 2009, 30(6): 1028-1034. (in Chinese)
本文引用 [1] 摘要

A concept design based on the rotating rib proposed by H.P.Monner is conducted to implement the variable camber adaptive wing concept by means of deforming the trailing edge flexibly with continued and smooth contour. A study is made of the kinematics of the rib structure, which can be simplified as a single degree- of freedom (DOF) leverage system constrained by pivot joints. The pivot location optimization by curve approximation is proposed to design the flexible trailing edge to meet the design requirements. To test the feasibility of the proposed concept design method, a 2D wing model characterized by NACA63015A airfoil with 1000 mm length in chordwise direction is utilized as a benchmark. The maximum deflection displacement of the tip point on the trailing edge as required by the design is 62 mm. Three types of cambered trailing edges with the same tip point deflection displacement but different deflection tracks, i.e., the beam type, the arc of circle type, and the inverse beam type, are introduced. A comparative study is performed in terms of structure realization, load carrying capability, and aerodynamic performance. The result shows that the model-configured with the arc of circle type trailing edge has the best performance and the design method is feasible and practical. It can be applied to any other design proposals of trailing edge deflection based on specific requirements.
[24]
CHEN Y J, YIN W L, LIU Y J, et al. Structural design and analysis of morphing skin embedded with pneumatic muscle fibers[J]. Smart Materials and Structures, 2011, 20(8): 085033.
https://doi.org/10.1088/0964-1726/20/8/085033
https://iopscience.iop.org/article/10.1088/0964-1726/20/8/085033
本文引用 [1]
[25]
冷劲松, 孙健, 刘彦菊. 智能材料和结构在变体飞行器的应用现状与前景展望[J]. 航空学报, 2014, 35(1): 29-45.
https://doi.org/10.7527/S1000-6893.2013.0265
摘要
变体飞行器可以根据不同的飞行条件改变自身形状以获得最优的气动性能，大大提高飞行器的综合性能，是未来飞行器发展的重要方向之一。新型智能材料和结构具有驱动、变形、承载、传感等特点，为变体飞行器的设计提供了新的技术途径。本文根据不同可变形机翼结构分类，详细阐述了智能材料和结构在自适应结构、智能驱动器和变形蒙皮等方面的研究现状。变体飞行器的实现亟需解决变形/承载一体化蒙皮技术、轻质大输出力驱动器技术和自适应结构技术等关键技术，本文还对智能材料和结构未来在变体飞行器上的应用前景进行了展望。
LENG J S, SUN J, LIU Y J. Application status and future prospect of smart materials and structures in morphing aircraft[J]. Acta Aeronautica et Astronautica Sinica, 2014, 35(1): 29-45. (in Chinese)
https://doi.org/10.7527/S1000-6893.2013.0265
本文引用 [1] 摘要

Morphing aircraft can alter their shapes to achieve optimal aerodynamic performance under different flight conditions, which will greatly improve the comprehensive performance of the aircraft. Their emergence and development is one of the most important trends of future aircraft. Smart materials and structures have the properties of actuating, morphing, loading, sensing etc., which provide a new technological approach to morphing aircraft design. In this paper, research status is elaborated of smart materials and structures in adaptive structures, smart actuators, and morphing skins. Some key technologies are addressed in detail, such as deformation/loading integrative skins, lightweight high-output actuators, and adaptive structures. The future prospect of the application of smart materials and structures in morphing aircraft is also discussed.
[26]
陈秀, 葛文杰, 张永红, 等. 基于遗传算法的柔性机构形状变化综合优化研究[J]. 航空学报, 2007, 28(5): 1230-1235.
摘要
实现机翼在不同的飞行状态下的最优气动外形是变弯度自适应机翼的一项关键技术。针对传统铰链机构会使机翼表面产生不连续变化而导致气流提早分离的问题，从全柔性机构实现连续平滑的形状变化的技术出发，以目标形状与实际形状的边界曲线之差最小为优化目标，采用遗传算法(GA)对柔性机构的拓扑、尺寸、形状进行了综合优化。在优化方法上，以二进制编码技术和实数编码技术为基础建立初始离散柔性机构的混合变量遗传算法模型，将其映射为有限元模型并进行了结构分析。在优化过程中引入了渐进结构优化(ESO)算法的思想，消除GA优化过程中产生的自由单元，改善了优化效率和分析结果。结合机翼前缘形状变化实例，基于MATLAB进行优化设计，并用ANSYS10.0对优化结果进行了机构的仿真分析。分析结果表明，所提出的方法合理、有效。
CHEN X, GE W J, ZHANG Y H, et al. Investigation on synthesis optimization for shape morphing compliant mechanisms using GA[J]. Acta Aeronautica et Astronautica Sinica, 2007, 28(5): 1230-1235. (in Chinese)
本文引用 [1]
[27]
徐钧恒, 杨晓钧, 李兵. 基于交叉簧片式铰链的变弯度机翼机构设计[J]. 浙江大学学报(工学版), 2022, 56(3):444-451, 509.
XU J H, YANG X J, LI B. Design of wing mechanism with variable camber based on cross-spring flexural pivots[J]. Journal of Zhejiang University (Engineering Science), 2022, 56(3): 444-451, 509. (in Chinese)
本文引用 [1]
[28]
王宇, 黄东东, 郭士钧, 等. 变体机翼后缘多学科设计与优化[J]. 南京航空航天大学学报, 2021, 53(3):415-424.
WANG Y, HUANG D D, GUO S J, et al. Multidisciplinary design and optimization of trailing edge of morphing wing[J]. Journal of Nanjing University of Aeronautics & Astronautics, 2021, 53(3): 415-424. (in Chinese)
本文引用 [1]
[29]
尉濡恺, 戴玉婷, 杨超, 等. 基于变弯度后缘的机翼阵风响应减缓数值研究[J]. 北京航空航天大学学报, 2023, 49(7):1864-1874.
WEI R K, DAI Y T, YANG C, et al. Numerical study of wing gust response alleviation based on camber morphing trailing edge[J]. Journal of Beijing University of Aeronautics and Astronautics, 2023, 49(7):1864-1874. (in Chinese)
本文引用 [1]
[30]
陈钱, 白鹏, 尹维龙, 等. 可连续光滑偏转后缘的变弯度翼型气动特性分析[J]. 空气动力学学报, 2010, 28(1): 46-53.
CHEN Q, BAI P, YIN W L, et al. Analysis on the aerodynamic characteristics of variable camber airfoil with continuous smooth morphing trailing edge[J]. Acta Aerodynamica Sinica, 2010, 28(1): 46-53. (in Chinese)
本文引用 [1]
[31]
MONNER H P. Realization of an optimized wing camber by using formvariable flap structures[J]. Aerospace Science & Technology, 2001, 5(7):445-455.
本文引用 [1]
[32]
聂瑞, 裘进浩, 季宏丽, 等. 主动柔性后缘气动特性优化[J]. 工程热物理学报, 2019, 40(1): 69-76.
NIE R, QIU J H, JI H L, et al. Aerodynamic characteristics optimization of active compliant trailing edge[J]. Journal of Engineering Thermophysics, 2019, 40(1): 69-76. (in Chinese)
本文引用 [1]
[33]
GU X J, YANG K K, WU M Q, et al. Integrated optimization design of smart morphing wing for accurate shape control[J]. Chinese Journal of Aeronautics, 2021, 34(1):135-147.
本文引用 [1]
[34]
GIL L, ANDREU A. Shape and cross-section optimisation of a truss structure[J]. Computers & Structures, 2001, 79(7): 681-689.
https://doi.org/10.1016/S0045-7949(00)00182-6
https://linkinghub.elsevier.com/retrieve/pii/S0045794900001826
本文引用 [1]
[35]
李宝仁, 刘军, 杨钢. 气动人工肌肉系统建模与仿真[J]. 机械工程学报, 2003, 39(7): 23-28.
摘要
建立了气动人工肌肉系统完整的静动态特性数学模型，提出气动人工肌肉系统的工作过程可以分为等容充气、充气收缩、排气伸长和等容排气四个部分。并通过仿真分析了气动人工肌肉系统的工作特性，为控制策略的选取以及试验研究打下基础。
LI B R, LIU J, YANG G. Modeling and simulation of pneumatic muscle system[J]. Chinese Journal of Mechanical Engineering, 2003, 39(7): 23-28. (in Chinese)
本文引用 [1]
[36]
王斌锐, 靳明涛, 沈国阳, 等. 气动肌肉肘关节的滑模内环导纳控制设计[J]. 兵工学报, 2018, 39(6): 1233-1238.
https://doi.org/10.3969/j.issn.1000-1093.2018.06.025
摘要
柔顺控制是共融机器人研究的重点。针对级联式气动肌肉肘关节动力学模型，建立了以滑模位置控制为内环、触力导纳控制为外环的控制结构；设计了带干扰观测器的滑模控制器（SMCDO），证明SMCDO算法的收敛性；将环境等效为弹簧模型，设计了外环导纳控制器，并给出控制律。搭建实物测试平台，分别开展阈值力、力安全阈值测试以及碰撞测试，并分析了刚度系数对修正轨迹和接触力的影响。实验结果表明：关节柔顺性与刚度系数相关；SMCDO内环导纳控制精度优于无干扰观测器的滑模控制器内环导纳控制；所设计的控制算法稳定且有效。
WANG B R, JIN M T, SHEN G Y, et al. Design of admittance control with sliding mode for elbow joint actuated by pneumatic muscle[J]. Acta Armamentarii, 2018, 39(6): 1233-1238. (in Chinese)
本文引用 [1]

64

Accesses

0

Citation

Detail
段落导航
相关文章

/

〈 〉