A Design Method of Vibration Accelerated Excitation Based on Feedback Approximate Damage

FENGYunwen, YANGRongji, XUEXiaofeng, LIUJiaqi, GAOTao

PDF(15182 KB)
CN Submission Journal Articles Figures Search
Adv. Search

  • Sponsored by: China Association for Science and Technology (CAST)

    Editor-In-Chief: Xu Yida

    ISSN 1000-1093

    　

  • Hosted By: China Ordnance Society

    Published By: Acta Armamentarii

    CN 11-2176/TJ

Acta Armamentarii, a Chinese monthly journal, was first published in 1979. The journal is supervised by China Association for Science and Technology, sponsored by China Ordnance Society，and edited and published by Editorial Board of Acta Armamentarii. The Journal is included in all important domestic databases，and also collected by Engineering Index (EI, USA), Chemical Abstracts (CA, USA), Science Abstracts (SA, UK）, Abstract Journal (AJ, Russia), and Current Bibliography on Science and Technology(CBST).Acta Armamentarii has been selected into the journal Of Ordnance Science and Technology (Weapons Industry) Field Of High Quality Scientific and Technological Periodical Classification Catalogue (2022 edition), ranking T1, and the journal of Automotive Engineering Field of High Quality Scientific and technological Periodical classification Catalogue, ranking T2.
PDF(15182 KB)
Acta Armamentarii ›› 2025, Vol. 46 ›› Issue (2) : 240138. DOI: 10.12382/bgxb.2024.0138

A Design Method of Vibration Accelerated Excitation Based on Feedback Approximate Damage

Author information +
History +

Abstract

The method for formulating the high-acceleration profiles for electromechanical products has some problems,such as unclear correlation between key element of profile and excitation failure mechanism,low fault excitation efficiency,and high testing costs.To establish a correlation mechanism between the cumulative damage and the key elements of vibration test profile,a vibration acceleration excitation design method based on feedback approximate damage is proposed.The refined design of vibration test profile is achieved through the dynamic control of damage increment.By integrating the analysis of vibration damage mechanism and the frequency-domain analytical technology of power spectral density,the mapping relationship between vibration excitation and cumulative damage is quantified,and a vibration excitation-damage corresponding model (CM-VED) is established.The validity of the proposed method is verified by taking the high-acceleration step vibration test of a fuse as an example.The research findings indicate that the obtained high-acceleration vibration test profile enhances the excitation accuracy of failure limit by 60% compared with the standard fixed-step method,and the time is shortened by 33.33% compared with that of the equal division method while ensuring high excitation accuracy.The proposed CM-VED can provide a theoretical basis for establishing the correspondence between excitation and damage.The proposed vibration acceleration excitation design method based on feedback approximate damage can reduce the test cost while guaranteeing the excitation accuracy,providing technical support for the design of the high-acceleration vibration test profile of electromechanical products.

Key words

high-acceleration test / approximate damage / vibration excitation / profile design / quantitative mapping

QR code of this article

Cite this article

EndNote

Ris (Procite)

Bibtex

Download Citations
FENG Yunwen , YANG Rongji , XUE Xiaofeng , LIU Jiaqi , GAO Tao. A Design Method of Vibration Accelerated Excitation Based on Feedback Approximate Damage. Acta Armamentarii. 2025, 46(2): 240138 https://doi.org/10.12382/bgxb.2024.0138

0 引言

高加速寿命试验(Highly Accelerated Life Testing,HALT)是一种通过逐级递增模拟环境应力,短时间快速暴露内部缺陷,进而发现产品设计极限的安全有效的试验方法[1-2]。HALT不仅可以快速找到产品的设计和破坏极限,分析改进产品设计界限范围,还可以在研发阶段筛选出设计缺陷并及时消除,从而提高产品的耐环境应力裕度及可靠性,缩短研发时间和成本[3-4]。
试验剖面设计技术直接决定HALT试验的效度,对模拟实际工作条件下的产品失效模式至关重要,一直是HALT试验领域亟待解决的关键问题之一[5⇓⇓-8],目前剖面设计方法多数延用恒定步长法[9⇓⇓-12]。然而,薛小锋等[13]、姬亚萌等[14]、Jakob等[15]、Kim等[16]和Tao等[17]通过研究表明,恒定步长法设计的试验剖面准确度及效率较低,应在考虑产品失效机理的基础上,通过优化设计加速激励水平以提高试验效率与精度,如Tao等[17]提出的基于热疲劳自适应的加速模型构建HALT剖面,可在提高试验结果的精度。因此,基于产品失效机理设计规划HALT试验剖面激励水平,有望提高试验效率与准确性。如Alex等[18]采用文献调研的方式,对基于不同激励条件下的失效机理构建的加速模型以及HALT试验技术进行了综合分析。Han等[19]基于双变量试验数据分析试验单元应力-寿命关系,确定各应力量级的寿命遵循韦伯分布,建立累积暴露模型(产品所受到的温度、湿度、化学腐蚀等各种应力影响,可按时间累积,对产品的总耐久性及可靠性产生影响),并通过优化模型参数的渐近方差确定最优的应力变化,形成最优试验方案。Ling等[20]针对一次性产品试验失效数据呈威布尔分布的特定,基于可靠性最大似然估计渐近方差最小化技术,提出一种步进应力加速寿命试验最优设计的方法。Yan等[21]通过D-优化和V-优化准则,优化基于Tweedie指数扩散过程的应力加速试验设计,给出最优试验设计方案的应力分布水平。Zhang等[22]从轴承振动信号中提取有效特征,通过调整每步卷积核的权重给出步长规划,提出了一种融合深度可分离卷积和空间随机失活正则化的步进试验设计方案。Wang等[23]利用遗传算法和蒙特卡洛模拟对应力水平和测试时间进行优化设计,构建了基于随机过程的恒定应力加速退化试验模型,并通过对自调温加热电缆的应用分析验证方法的有效性。Czerny等[24]探究了典型复杂机电产品振动疲劳损伤与剖面步长的相关性,提出了损伤作为控制变量以优化试验设计的设想。
以上学者在对试验剖面进行加速激励设计时依赖于大量试验获取失效数据,这一过程伴随着显著的试验资源消耗,如Han等[19]、Ling等[20]、Yan等[21]基于大量试验数据分析失效数据分布规律,Zhang等[22]通过大量轴承振动试验提取有效特征;上述方法主要从统计学的视角出发,对失效数据进行分布规律的数学建模,如Ling等[20]、Yan等[21]分别采用威布尔分布、Tweedie指数分布对失效数据进行分析,而Han等[19]、Zhang等[22]、Wang等[23]则分别依据方差分析、深度可分离卷积分析、蒙特卡洛模拟来设计最优化的试验激励设计方案,这些方法虽在数学上提供了对失效数据的深入理解,但并未涉及产品在特定激励条件下的失效机制,相对而言,Tao等[17]的研究通过考虑温度激励下的热疲劳现象,结合载荷分布特性,较为深入地探讨了失效机理进而构建的试验剖面更具针对性和准确性。Czerny等[24]及文献[25-26]虽指出损伤会随着振动载荷的步进而叠加,并建议在振动加速试验的激励优化设计中,将累积损伤作为一个关键的失效考量因子,却并未论述累积损伤与试验剖面之间的具体关联机制,也未提供损伤数据与试验剖面之间的转换方法。
为研究振动高加速试验设计中累积损伤与关键要素之间的定量关联机制,本文结合振动损伤机制分析与功率谱密度频域解析技术,建立了振动激励-损伤对应规划模型(Vibration Excitation-Damage Corresponding Model,CM-VED),为振动激励和累积损伤之间建立了定量的映射关系;为精准实现损伤数据与试验剖面之间的转换,提出一种基于反馈近似损伤的振动激励设计方法,通过动态控制损伤增量,实现对振动试验剖面的精细化设计。

1 基于反馈近似损伤的振动加速激励设计

1.1 基于反馈近似损伤的振动加速激励设计方法

1.1.1 建立CM-VED

为建立振动激励与累积损伤之间的量化映射关系,通过融合振动损伤理论与功率谱密度(Power Spectral Density,PSD)频域分析,建立了CM-VED,如图1所示,进一步提出反馈近似损伤法精确控制每步振动试验中损伤增量,以实现对载荷步长的精确调节。
Fig.1 CM-VED model

图1 CM-VED模型

Full size|PPT slide

1.1.2 反馈近似损伤法约束条件

在已知累积损伤随振动载荷变化趋势的基础上,为了精准实现损伤数据与试验剖面之间的转换,提出了反馈近似损伤法,利用迭代反馈控制策略,精确调控每一振动步骤中的损伤增量,从而实现对振动载荷的逐步精确控制。反馈近似损伤法的约束为尽可能使每步振动载荷造成的损伤值的增量近似。准则如下:
1)剖面呈现形式。由CM-VED可知,累积损伤随振动载荷呈指数增长趋势,使试验每步损伤值增量近似,则试验前期步长增量大,试验后期步长增量小,试验前期大步进可更快地达到目标损伤值,节省试验时间和资源,试验后期小步进可准确确定破坏极限范围,在试验中期保持每步累积损伤增量近似,可实现变步长法过渡阶段步长的合理量化。试验各阶段损伤增量变化趋势见图2。
Fig.2 Change trend of damage increment in each stage of high-acceleration test

图2 高加速试验各阶段损伤增量变化趋势

Full size|PPT slide

2)保证失效机理不变。高加速寿命标准指南[27-28]规定要保持振动HALT试验过程中失效机理不变,尽可能保持每步损伤值增量近似,可以更准确地评估材料或结构在振动环境下的损伤失效性能,若每步损伤值相差较大,可能会导致对材料或结构损伤性能变化,导致失效机理改变。

1.1.3 反馈近似损伤法思路

基于CM-VED,以每步损伤增量近似为约束,以HALT试验标准指南规定的步长增量范围为限制条件(如国家标准GB/T 29309电工电子产品加速应力试验规范[27]及Qualmark HALT 试验指南[28]对振动HALT试验步进增量规定在2~5Grms内),提出反馈近似损伤法以设计剖面步长,反馈近似损伤法思路如图3所示,具体步骤如下:
Fig.3 Feedback approximate damage method

图3 反馈近似损伤法思路

Full size|PPT slide

1)初始规划。以总累积损伤等于1为目标值,使每步损伤增量近似,初步规划出每步步长取值;
2)标准限制。将规划的步长与HALT试验标准指南规定的上、下限进行逐步比较,若超出限制区间,则将步长逐级强制调整为区间上、下限;
3)反馈迭代过程。将步长逐级调整后,程序反馈总累积损伤不为1,保留前i步已强制调整的步长,更新剩余步长的损伤增量以逐级迭代剩余步长,使累积损伤和为1的目标值不变;
4)输出结果。判断反馈迭代的结果是否满足振动失效条件,若不满足则返回步骤2进行下一步的反馈迭代,若满足则输出步长i+1次反馈迭代结果作为试验优化设计方案,且第i+1步长为破坏极限预估值。
反馈近似损伤法对试验剖面每步步长进行逐级迭代,设计出的试验剖面可在提高试验精度以及试验效率,并实现试验中期过渡阶段步长的合理量化,自适应调整各步步长。

1.2 基于反馈近似损伤的振动加速激励设计流程

为了合理有效的规划振动HALT试验剖面,本文基于各级振动载荷下累积损伤变化趋势,提出反馈近似损伤法设计振动HALT试验剖面,其流程(见图4)为:
Fig.4 Design process of vibration acceleration excitation based on feedback approximate damage

图4 基于反馈近似损伤的振动加速激励设计流程

Full size|PPT slide

1)通过故障模式影响分析(Failure Modes and Effects Analysis,FMEA)进行产品故障定位,再根据产品的可靠性框图及故障树梳理产品与内部元件失效逻辑。
本文以引信装置为代表的串联型电子设备作为案例对象,通过同类型产品的振动试验结果[29],明确振动激励下该类型产品失效的根本原因为元器件累积损伤失效。通过故障树分析方法[30-31]分析引信失效逻辑(见图5),引信及其模块只用到或门一种逻辑门符号,系统及其模块之间为简单串联关系,任一底事件对应的元件失效,即会导致模块失效,进而导致产品功能失效,产品的破坏极限由抗振动极限低的元件或模块决定。
Fig.5 Fault tree of a certain fuse detonation system

图5 某型引信起爆系统故障树

Full size|PPT slide

2)基于Nelson等效累积法则、Miner累积损伤模型、PSD函数频域分析等基础理论构建CM-VED,并通过HALT随机振动步进仿真及实际试验数据验证模型的正确性。
其中,本文振动损伤理论采用了Steinberg提出的一种基于高斯分布和Miner线性累积损伤理论的三区间法[32],从概率的角度对疲劳寿命进行分析。
D=n1σN1σ+n2σN2σ+n3σN3σ=0.6831f0TN1σ+0.271f0TN2σ+ 0.0433f0TN3σ
(1)
式中:D为结构疲劳损伤门槛值;n1σ、n2σ、n3σ为1σ、2σ、3σ应力情况下的循环次数;N1σ、N2σ、N3σ为1σ、2σ、3σ应力情况下的破坏循环数;f0为von Mises应力的统计平均频率;T表示随机响应的作用时间。当循环累积损伤在不同应力水平下达到D时,结构将发生疲劳破坏。工程应用中的大量随机振动疲劳试验表明,Miner疲劳准则设定的疲劳门槛值接近1。
3)基于CM-VED,利用迭代反馈控制策略,提出反馈近似损伤法优化振动HALT试验剖面步长设计,结合高加速寿命试验标准指南[27-28]确定振动HALT试验剖面各要素,设计剖面制定方法。
4)通过某型引信振动步进试验验证步长及剖面制定方法的正确性,并与传统的步长设计方法进行对比,验证所提方法的有效性。
系统故障树分析所用到的逻辑符号见表1。
Table 1 Fault tree logic gates and event symbols

表1 故障树逻辑门、事件符号

符号 名称 含义
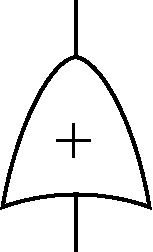或门 输入端只要有一个事件出现时即有输出
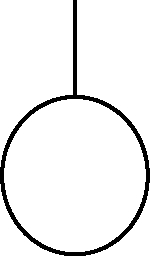基本事件 导致顶事件发生的最基本的或不能再向下分析的原因,是底事件的一种
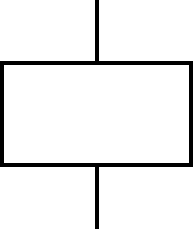结果事件 由其他事件或事件组合导致的事件,分为顶事件和中间事件

2 CM-VED原理

为建立振动激励与累积损伤之间的量化映射关系,本章节基于振动高加速试验对输入激励、每步停留时间的规范要求,首先通过Nelson等效累积法则与Miner累积损伤三区间理论相结合推导累积损伤与应力均方根值的关系式;然后通过PSD函数频域分析法推导振动载荷与应力均方根值的关系式;最后结合上述两关系式推导累积损伤值与各级随机振动载荷之间的函数关系式,并用振动步进仿真数据验证CM-VED的正确性。

2.1 累积损伤与应力均方根值关系确定

在随机振动载荷作用下,复杂机电产品元件管脚等处会出现裂纹直至疲劳开裂,主要由弹性范围内的高周应力疲劳造成[33],疲劳寿命可由式(2)表示:
Ni=N0S0Sib
(2)
式中:Ni为机电产品上某一测试点持续状态的疲劳寿命,i为机电产品上的测试点编号;Si为应力均方根值;N0为参考点寿命;S0为参考点应力均方根值;b为应力-寿命(S-N)曲线斜率,表示材料疲劳强度随循环次数的变化速率。
结合第1节所述的Miner累积损伤三区间理论,可将式(1)变换为
Di=n1σN1σ+n2σN2σ+n3σN3σ=0.6831f0TN0S0Sib+0.271f0TN0S02Sib+0.0433f0TN0S03Sib
(3)
就引信产品而言,其振动HALT试验输入激励为功率谱密度曲线,当输入的振动量级改变时,仅会导致PSD函数幅值变化,不会导致谱型变化。因此f0表示的von Mises应力的统计平均频率不变,式(3)简化为
Di=f0TN0S0Sib(0.6831+0.271×2b+0.0433×3b)
(4)
根据高加速寿命试验标准指南[27-28]及引信相关标准规定,引信振动高加速试验剖面的每步停留时间均为10min,即T表示的随机振动载荷作用时间不变,基于式(4)可得到累积损伤与应力均方根值的比例关系式:
D2D1=f0TN0S0S2b(0.6831+0.271×2b+0.0433×3b)f0TN0S0S1b(0.6831+0.271×2b+0.0433×3b)=S2S1b
(5)

2.2 振动载荷与应力均方根值关系确定

在工程领域,确定结构某测试点(c点)的应力PSD函数常通过以下关系式:
Gc(f)=Wa(f)Hca2(f)
(6)
式中:f为频率;Wa(f)为作用在a点的激励PSD函数;Hca(f)为结构在a点处激励c点处响应的频响函数。
PSD函数的n阶惯性矩定义为
mn=∑i=1∞f inGc(f i)Δf
(7)
式中:fi为机电产品上某一测试点的频率值,范围由振动载荷谱的频率区间决定;Δf为不同点之间的频率差值。
由0阶惯性矩得到应力响应和输入激励的均方根值分别为
SRMS=m0=∑i=1∞Wa(fi)Hca2(fi)Δf
(8)
gRMS=∑i=1∞Wa(fi)Δf
(9)
设x、y、z为试验件外载荷施加的3个轴向,三者相互独立,gx,RMS、gy,RMS、gz,RMS分别为三轴输入激励的均方根值,施加三轴振动激励时,由式(8)和式(9)得到测试点的等效应力响应为
SRMS=α(gx,RMS)2+β(gy,RMS)2+γ(gz,RMS)2
(10)
式中:α、β、γ分别为频响函数和激励谱形状对von Mises等效应力的影响。当试件、测试点和输入功率谱密度曲线确定时,参数α、β、γ是恒定的。
由式(10)可得到单轴振动激励的情况下振动载荷与应力均方根值关系式:
SRMS2SRMS1=gRMS2gRMS1
(11)

2.3 CM-VED及验证

由式(10)得到三轴振动载荷与应力均方根值的比例关系:
SRMS2SRMS1=α(gx,RMS2)2+β(gy,RMS2)2+γ(gz,RMS2)2α(gx,RMS1)2+β(gy,RMS1)2+γ(gz,RMS1)212
(12)
结合式(5)与式(12)可得到三轴激励下累积损伤值与各级随机振动载荷之间的比例关系式:
D2D1=α(gx,RMS2)2+β(gy,RMS2)2+γ(gz,RMS2)2α(gx,RMS1)2+β(gy,RMS1)2+γ(gz,RMS1)2b2
(13)
由式(13),在三轴振动激励下,任一振动载荷量级下的累积损伤值D与三轴输入振动激励的对应关系,即三轴加速度的多自由度振动环境下的CM-VED为
D=C[α (gx,RMS)2+β (gy,RMS)2+γ (gz,RMS)2]b2
(14)
式中:C为与结构固有特性及振动HALT试验每步停留时间有关的一个常数。
由式(14)可得,单轴激励下任一振动载荷量级下的累积损伤值D与振动激励gRMS为指数关系,CM-VED为
D=KgRMSb
(15)
式中:K为与结构固有特性及振动HALT试验每步停留时间有关的一个常数。
因此,本文建立的CM-VED既适用于三轴加速度的多自由度振动环境,也适用于单轴振动环境。对单轴激励下的CM-VED展开验证及应用研究,理由如下:
1)单轴CM-VED是建立三轴多自由度CM-VED的基础前提,由于三个轴向相互垂直、独立[34],式(14)三轴多自由度CM-VED中各轴向的影响参数α、β、γ须通过单轴CM-VED逐个确定。
2)引信试验标准规定以单轴进行振动试验:
①振动激励应沿着被试引信相互垂直的3个轴中的每一个轴向施加。目的在于确定引信的敏感方向,暴露各敏感方向下的薄弱部位,实现引信可靠性增长。
②引信振动试验须以引信振动环境对应的随机振动谱作为输入激励。但一般的三轴振动台只能对振动的总量级进行控制,无法输入随机振动谱,而单轴振动台可以输入随机振动谱,因此引信多以单轴振动进行试验。
因此,本文对单轴激励下的CM-VED展开验证及应用研究。模型验证如下:
文献[35]对航天精密机电组件开展高加速振动步进分析,通过振动仿真提取薄弱部位等效应力及累积损伤值,并通过实际HALT随机振动试验验证仿真结果的正确性。以3Grms步进递增,每个振动量级保持10min,仿真及实际试验结果表明,振动量级达到23Grms时机电组件大电容管脚完成断裂发生疲劳失效,检测结果见表2。
Table 2 Analyed results of large capacitance stress and cumulative damage

表2 大电容应力、累积损伤分析结果

振动载荷/
Grms		 元器件最大等效应力值/MPa 各级载荷下的
损伤
1σ 2σ 3σ
5 20.3 40.6 60.9 1.059×10-4
8 32.6 65.2 97.8 1.799×10-3
11 44.8 89.6 134.4 0.0120
14 56.9 113.8 170.7 0.0503
17 69.2 138.4 207.6 0.1620
20 81.5 163.0 244.5 0.4310
21 85.5 171.0 256.5 0.5740
22 89.6 179.2 268.8 0.7600
从表2中任取一组累积损伤值,例如当随机振动载荷取20Grms时,随机振动10min,损伤值为0.431,代入CM-VED式(15),D=0.431,gRMS=20,金属管脚材料为铜镀锡,b=5.98,可求解出K的值:
K=DgRMSb=0.431205.98=7.150×10-9
(16)
因此可得出大电容在各级载荷下随机振动10min的CM-VED:
D=7.150×10-9×gRMS5.98
(17)
通过将表2中的大电容各级载荷累积损伤值与式(17)大电容CM-VED进行对比,对比如图6所示,大电容的随机振动累积损伤数据点与CM-VED近乎拟合,最大对比误差Er,max=2.15%,平均对比误差 Er¯=0.672%,所提CM-VED拟合效果较好。
Fig.6 Comparison chart between accumulated damage data of large capacitors and CM-VED

图6 大电容累积损伤数据与CM-VED对比

Full size|PPT slide

3 基于反馈近似损伤法试验剖面设计

3.1 反馈近似损伤法激励步长设计

反馈近似损伤法的基本思路是:首先确定期望目标、起始条件;其次根据累积损伤失效条件及CM-VED得出初步步长设计,根据HALT试验标准指南规定的限制条件,将累积损伤和与目标值逐级反馈比对,并依次迭代更新每步步长;最后选取迭代结果符合累积损伤失效条件的每步步长取值作为试验步长设计方案并输出迭代的最后一步步长作为破坏极限预估值。反馈近似损伤法设计剖面步长流程(见图7)为:
Fig.7 Process of designing the profile step size by feedback approximate damage method

图7 反馈近似损伤法设计剖面步长流程

Full size|PPT slide

步骤1 根据1.1节基于反馈近似损伤的振动加速激励设计方法,反馈近似损伤法以尽可能保证每步损伤增量近似为出发点及约束。
步骤2 起始条件设置,设定每步累积损伤增量相等,设为ΔD,输入期望步进次数K,每步造成的累积损伤值为Di,i=1:K。
步骤3 根据累积损伤失效条件,K步振动造成累积损伤和为1,即D1+D2+D3+…+DK=1→ΔD+2ΔD+3ΔD+…+KΔD=1,计算出每步累积损伤增量ΔD=2/K(K+1)。
步骤4 根据CM-VED D=K gRMSb,可由每步损伤Di得到每步步长:
 f(Di)=gRMSi=Di/Kb
(18)
式中:f(·)为损伤值D与振动载荷幅值gRMS之间的函数关系;gRMSi为各步载荷大小。
步骤5 高加速寿命试验标准指南[27-28]对振动HALT试验步进应力步长的规定:全轴随机振动步进试验以2~5Grms的振动应力增量增加。根据规定需验证步骤 4 初步设计的每步步长取值是否符合国标限制:2Grms≤f(Di+1)-f(Di)≤5Grms,若符合限制条件则保留f(Di)作为第i步步长,若不符合则进入步骤6。
步骤6 若每步步长增量大于5Grms,或小于2Grms,则将第i步步长增量强制调整为5Grms或2Grms,即f(Di+1)=f(Di)+5Grms或f(Di+1)=f(Di)+2Grms,并保留f(Di+1)作为第i+1步步长。
步骤7 反馈迭代过程,经步骤 6步长调整后,K步振动造成的累积损伤和不为1,即 ∑i=1KDi≠1,计算累积损伤与目标值1之间的差值,调整每步累积损伤增量ΔD及第i-K步损伤Di-DK的值,使累积损伤和为1的目标值不变:
ΔD=2×1-∑j=1iDj-(K-i)Di+1(K-i)(K-i-1)
(19)
Di+1=Di+ΔD
(20)
步骤8 判断反馈迭代过程中前i+1步累积损伤和是否大于1,若小于1,则令i=i+1并返回步骤5进行下一个步长的反馈迭代,直至前i+1步累积损伤和大于1,进入步骤 9。
步骤9 输出满足步骤 8 的i+1次迭代结果作为高加速试验每步步长优化设计方案,且由于前i+1步累积损伤和大于1,可知第i+1步步长f(Di+1)即为破坏极限预估值,最后运用Stairs函数绘制振动步进剖面图。

3.2 振动HALT试验剖面关键要素确定

通常的振动HALT试验剖面由起始应力、每步停留时间、步长等要素组成,目的是指导试验的应力加载以及应力的停留时间,以便暴露故障并快速有效地进行试验。采用反馈近似损伤法在剖面中加入步长设计方案及破坏极限预估值,以更好地预计产品发生故障的应力量级,剖面设计框架如图8所示。
Fig.8 Design framework for vibration HALT test profile

图8 振动HALT试验剖面设计框架

Full size|PPT slide

通过有限元随机振动仿真分析得到产品的应力响应,基于CM-VED,结合反馈近似损伤法设计剖面步长并得到产品破坏极限预估值,剖面要素中的起始应力、停留时间及施加方式根据产品实况、任务剖面及高加速寿命试验标准指南给出。
剖面确定方法具体如下:
1)起始应力/应力步长。根据高加速寿命试验标准指南[27-28],振动步进起始应力设置值及每步步长增量均为2~5Grms,因此可将起始应力视为步长设计的第一步,由反馈近似损伤法设计取值。
2)每步停留时间。根据高加速寿命试验标准指南[27-28]以及引信相关标准规定,每个振动应力水平的停留时间一般为10min。
3)应力施加方式。根据高加速寿命试验标准指南[27-28],应力输入振动PSD曲线,频率范围从最低频20Hz到最高频2kHz,振动方向包括x轴、y轴、z轴三个轴向。
4)预测破坏极限。根据反馈近似损伤法最后一步步长即可作为元器件破坏极限预估值,由第1节引信故障树分析,引信与内部元件为串联关系,元器件破坏极限预估值即为引信破坏极限预估值,产品的破坏极限由抗振动极限低的元件或模块决定。

4 案例验证

4.1 工况分析

以某型引信起爆控制模块作为研究对象,首先根据该产品可靠性框图及故障树分析明确产品失效逻辑;其次,根据产品FMEA、产品内部结构模块得出产品故障模式分析表,明确产品故障模式及其串联的元器件类型。
案例引信外观及内部功能模块设计见图9,功能模块中的元器件名称对应表见表3。
Fig.9 Design of appearance and internal structural modules of a certain fuse

图9 某型引信外观及内部结构模块设计

Full size|PPT slide

Table 3 Corresponding table of internal structure module component names

表3 内部结构模块元器件

标号 元器件名称 标号 元器件名称
A 场控晶闸管(MOS Controlled Thyristor,MCT) G 电压比较器b
B 金属氧化物半导体场效应晶体管(Metal Oxide Semiconductor Field Effect Transistor,MOSFET) H 二极管
C 电压比较器a I 贴片电阻
D A/D转换器 J 变压器
E 信号调理器 K 陶瓷电阻
F 升压芯片、降压芯片 L 三极管
该引信系统共有4个功能模块单元,各单元在电路功能上相对独立,系统及其模块之间为简单串联关系,产品可靠性框图如图10所示。
Fig.10 Reliability block diagram of a certain fuze

图10 某型引信可靠性框图

Full size|PPT slide

基于产品可靠性框图,结合产品FMEA分析明确模块单元异常所导致的产品故障模式以及故障模式造成的局部影响及最终影响;结合图9的产品内部功能模块设计,明确模块单元所串联的元器件类型,元器件损坏即会导致模块单元功能异常,进而导致产品故障,基于此列出产品故障模式分析见表4。
Table 4 Analysis table for fault modes of a certain fuze

表4 某型引信故障模式分析表

故障
模式		 局部
影响		 最终
影响		 故障原因 串联元器件类型
电压
变换
异常		 高压点
火电路
不能正
常点火		 引信
瞎火		 高压变化
单元异常		 变压器、二极管、贴片电阻、升压芯片
反馈控制
单元异常		 MCT、比较电路芯片a、A/D转换器、信号调理器
发火
储能
不足		 雷管
无法
起爆		 引信
瞎火		 储能电路
单元异常		 贴片电阻、二极管、三极管
起爆触发
单元异常		 陶瓷电阻、MOSFET、比较电路芯片b

4.2 引信CM-VED

2.3节构建了CM-VED D=K gRMSb,b可由材料手册给出,K为与结构固有特性及振动HALT试验每步停留时间有关的一个常数,可通过一组已知的振动载荷与损伤数据反推得出。
本文针对4.1所述的某型引信起爆控制模块模型,采用振动仿真结合Miner线性累积损伤理论的三区间法的方式,求出该引信振动载荷与累积损伤数据,进而确定引信CM-VED。具体步骤如下:
1)模态分析。对引信模型进行模态仿真分析,提取固有频率及振型,并将分析结果与功率谱密度分析相结合,进行随机振动分析。
2)随机振动分析输入。引信相关标准规定的适用于引信振动环境试验的随机振动谱型作为输入激励,振动谱参数见图11,保持功率谱密度曲线形状不变,通过改变功率谱密度曲线幅值来改变振动量级[36],输入5~30Grms功率谱密度曲线作为输入激励。
Fig.11 Vibration power spectral density curve

图11 振动功率谱密度

Full size|PPT slide

图11中,倍频程oct定义为频率之间相差一倍的区间,dB/oct表示频率每增加一个倍频程,功率或幅度以dB为单位增加或减少的幅度。
3)随机振动仿真结果。计算基础激励参与因子,利用模态合并法将模态分析结果合并,求解出引信结构1σ~3σ等效应力响应及应力云图。图12为该引信在x轴向20Grms振动载荷下的引信等效应力云图,最大等效应力位于连接大陶瓷电阻与电路板之间的管脚处。
Fig.12 Equivalent stress cloud map of fuze under 20Grms load along x-axis

图12 x轴20Grms载荷下引信等效应力云图

Full size|PPT slide

4)计算累积损伤值。提取大陶瓷电阻在x轴向5~30Grms下的最大等效应力值,并通过Miner累积损伤三区间理论进行累积损伤计算,根据3.2节确定振动HALT试验每步停留时间为10min,计算结果见表5。
Table 5 Maximum equivalent stress and damage value of large ceramic resistor pin (x-axis)

表5 大陶瓷电阻管脚最大等效应力、损伤值(x轴)

振动载荷/
Grms		 元器件最大等效应力值/MPa 各级载荷
下的损伤		 合计损
伤值
1σ 2σ 3σ
5 17.136 34.272 51.408 3.840×10-5 0.768
10 34.295 68.590 102.885 0.00240
15 51.439 102.878 154.317 0.0275
20 68.590 137.180 205.770 0.154
25 85.744 171.488 257.232 0.584
30 102.890 205.780 308.670 1.738 2.510
5)构建引信CM-VED。根据4.1节对该引信的失效逻辑分析,该引信系统及其模块为串联关系,大陶瓷电阻损坏会引起起爆触发单元异常进而导致发火储能不足,因此大陶瓷电阻管脚CM-VED即为该引信的CM-VED。模型构建步骤如下:由表5任取一组累积损伤值,当随机振动载荷为20Grms时,随机振动10min,损伤值为0.154,代入2.3节所述的CM-VED式(15),D=0.154,gRMS=20,金属管脚材料为铜镀锡,b=5.98,可求解出K的值:
K=DgRMSb=0.154205.98=2.5548×10-9
(21)
因此可得出引信在x轴向各级载荷下随机振动10min的CM-VED为
D=2.5548×10-9×gRMS5.98
(22)
模型图见图13。
Fig.13 CM-VED of a certain fuse

图13 某型引信CM-VED

Full size|PPT slide

4.3 反馈近似损伤法设计剖面步长

基于引信CM-VED,结合反馈近似损伤法设计剖面步长,首先分析步进次数最小值与最大值,确定期望步进次数K的取值范围。
根据3.1节所提及,引信振动HALT试验每步增量限制为2~5Grms,因此以2Grms的增量步进直至累积损伤大于1时的步进次数即为最大步进次数,见式(23):
∑i=1nDi=∑i=1n2.5548×10-9×(i×2)5.98]
(23)
当步数n=11时, ∑i=111Di=0.57751,当步数n=12时, ∑i=112Di=1.03571。
由此可知Ns,max=12,同理以5Grms的增量步进直至累积损伤大于1时的步进次数即为最小步进次数,同表5,Ns,in=6。因此可确定期望步进次数K的取值范围为[6,12],具体取值可根据产品实际情况以及试验设计单位的要求进行选择,步长小会导致试验成本的浪费,步长大会导致破坏极限激发精度低。
本文以取区间中点NE=9作为输入,在保证准确度的同时兼顾试验成本。通过3.1节所述的反馈近似损伤法设计剖面步长。试验剖面如图14所示,表6为步长划分结果。
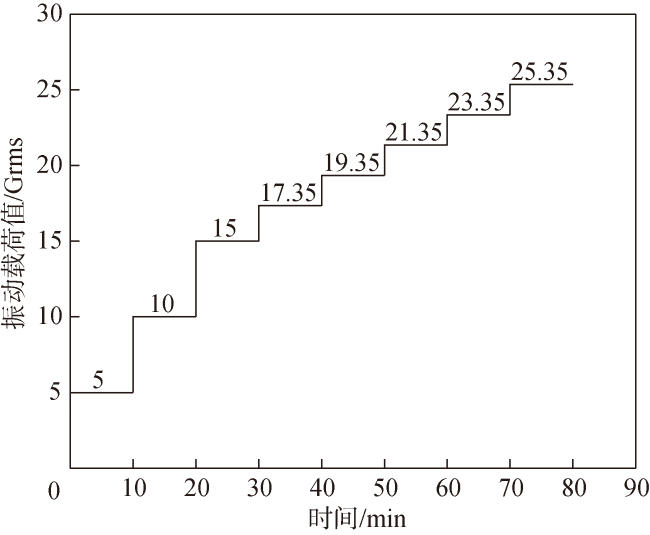
Fig.14 Test profile designed by feedback approximation damage method

图14 反馈近似损伤法设计的试验剖面图

Full size|PPT slide

Table 6 Profile step division of feedback approximate damage method

表6 反馈近似损伤法剖面步长划分

步进顺序 振动载荷/Grms 各级载荷下的损伤 合计损伤值
1 5.00 3.865×10-5 0.839
2 10.00 0.00240
3 15.00 0.0276
4 17.35 0.0659
5 19.35 0.1270
6 21.35 0.2280
7 23.35 0.3890
8 25.35 0.6360 1.468
由图14和表6可知,反馈近似损伤法设计的试验剖面步长先以5Grms的步长增量步进3步,再以2.35Grms的步长增量步进1步,最后以2Grms的步长增量步进4步,当引信以25.35Grms载荷振动10min时累积损伤值达到1.468>1,因此预测破坏极限区间为[23.35Grms,25.35Grms],步进次数为8次,试验时间为8次×10min=80min。

4.4 反馈近似损伤法剖面步长划分试验验证

采用反馈近似损伤法对该引信进行随机振动步进试验,图15所示为该产品振动HALT试验,图15(a)为弹轴方向(z轴)振动的固定方式,图15(b)为x轴、y轴向振动的固定方式,图15(c)为振动激励输入设备,图15(d)为信号检测设备。
Fig.15 Vibration HALT test of a certain fuse

图15 某型引信振动HALT试验

Full size|PPT slide

将反馈近似损伤法设计的振动试验剖面作为输入激励,见图16,振动量级为5~25.35Grms,每步振动10min,并实时检测产品模块输出的功能信号。
Fig.16 Vibration step test profile

图16 振动步进试验剖面

Full size|PPT slide

在进行振动试验前,对该引信功能信号进行检测,如图17所示,其中图17(a)为非振动情况下产品充电波形,图17(b)为放电波形,该引信充放电功能正常。
Fig.17 Product test results under non-vibration conditions

图17 非振动情况产品测试结果

Full size|PPT slide

将该引信置于振动台上,进行x轴向的振动HALT试验,当振动应力稳定驻留10min后,在该量级的振动应力下对产品进行在线功能测试。将产品置于19.35Grms及21.35Grms量级的载荷下各振动10min,测试输出信号,分别见图18(a)和图18(b),示波器采集到的信号与该产品非振动下的输出信号一致,产品模块功能正常。将振动量级调至23.35Grms,示波器采集到前、主级两级延时时间为692.5μs的输出信号,见图18(c),该延时时间在合格范围内,因此产品模块功能正常。将振动量级调至25.35Grms,通电测试其输出信号,示波器无信号,无法实现正常放电,见图18(d),该产品模块功能故障,恢复到上一级振动应力继续试验,功能仍然异常,停止试验。
Fig.18 x axis vibration HALT test fuse discharge curve

图18 x轴向振动HALT试验引信放电曲线

Full size|PPT slide

产品x轴向试验振动载荷量级与测试结果见表7,确定产品模块的振动破坏极限在23.35~25.35Grms之间。
Table 7 Test vibration load and test results

表7 试验振动载荷与测试结果

步进顺序 试验振动载荷/Grms 步长/Grms 测试结果
1 5 5 正常
2 10 5 正常
3 15 5 正常
4 17.35 2.35 正常
5 19.35 2 正常
6 21.35 2 正常
7 23.35 2 正常
8 25.35 2 异常
9 23.35 -2 异常
停止试验后,卸下引信,拆开产品外壳,解除灌封保护材料,观察产品故障部位。由图19(a)可见,产品电路模块中的大陶瓷电阻管脚发生断裂,通过电镜从侧面观察该断裂部位,可见其形成贯穿裂纹,如图19(b)所示,造成大陶瓷电阻功能异常。结合表4引信故障模式分析表可知,大陶瓷电阻故障会导致产品发火储能不足,即导致产品放电异常。
Fig.19 Cracks in the pins of large ceramic resistors caused by vibration tests

图19 振动试验引起大陶瓷电阻管脚裂纹

Full size|PPT slide

依据反馈近似损伤法仿真计算得出的产品破坏极限及故障模式,与依据反馈近似损伤法设计的剖面进行振动HALT试验得出的结果吻合,即图12振动仿真结果与图19振动试验结果一致,具有一定的指导意义与可信性。

4.5 步长方案对比

高加速寿命试验的步长划分有标准固步法与均分法两种,分别如下:
1) 标准固步法为参考了文献[23],产品起始振动量级设置为5Grms,步进步长设置为每步增量上限5Grms,每个振动量级保持10min,标准固步法由于步长跨步大,暴露故障的速度较快,但破坏极限的激发精度较低。
2) 均分法参考同类型产品的破坏极限,将其作为破坏极限估值,将估值与起始应力的差值均分10次得到每步步长[10],根据4.3节中表6反馈近似损伤法剖面步长划分可知,预测破坏极限为25.35Grms,起始应力为5Grms,因此由均分法可得每步步长为2Grms,恰好为每步增量下限。
现按照标准固步法,以5Grms步进步长对引信进行x轴向的振动仿真,并计算大陶瓷电阻管脚在各振动量级保持10min下的损伤值,最后记录累积损伤值符合失效条件时的每步步长取值作为试验步长设计方案。标准固步法设计的步长划分见表8,试验剖面见图20。
Table 8 Divided profile step size of standard fixed step method

表8 标准固步法剖面步长划分

步进顺序 振动载荷/Grms 各级载荷下的损伤 合计损伤值
1 5 3.840×10-5 0.768
2 10 0.00240
3 15 0.0275
4 20 0.1540
5 25 0.5840
6 30 1.7380 2.510
Fig.20 Experimental profile designed using standard fixed step method

图20 标准固步法设计的试验剖面图

Full size|PPT slide

将标准固步法设计的振动试验剖面作为试验输入激励,将该引信置于振动台上,进行x轴向的振动HALT试验,振动量级为5~30Grms,每步振动10min,并实时检测产品模块输出的功能信号。当产品所受载荷量级达到25Grms时,保持振动应力驻留10min,测试输出信号,见图21(a),示波器采集到的信号与该产品非振动下的输出信号一致,产品模块功能正常。将振动量级调至30Grms,通电测试其输出信号,示波器无信号,无法实现正常放电,见图21(b),该产品模块功能故障,恢复到上一级振动应力继续试验,功能仍然异常,停止试验。
Fig.21 Discharge curve of vibration HALT test fuse under standard fixed step profile

图21 标准固步法剖面下的振动HALT试验引信放电曲线

Full size|PPT slide

产品x轴向试验振动载荷量级与测试结果见表9,确定产品模块的振动破坏极限在25~30Grms之间。
Table 9 Test vibration load and test results of standard fixed step method

表9 标准固步法试验振动载荷与测试结果

步进顺序 试验振动载荷/Grms 步长/Grms 测试结果
1 5 5 正常
2 10 5 正常
3 15 5 正常
4 20 5 正常
5 25 5 正常
6 30 5 异常
7 25 -5 异常
停止试验后,解除引信保护结构,观察产品故障部位,如图22所示,产品电路模块中的大陶瓷电阻管脚发生断裂,故障部位与图12振动仿真结果及图19反馈近似损伤法试验结果一致。
Fig.22 Cracks in the pins of large ceramic resistors caused by standard fixed step vibration test

图22 标准固步法振动试验引起大陶瓷电阻管脚裂纹

Full size|PPT slide

综合上述标准固步法仿真及试验结果,标准固步法步进次数为6次,试验时间为6次×10min=60min,故障部位为大陶瓷电阻,破坏极限区间为[30Grms]。
按照均分法,以2Grms步长进行振动仿真,计算累积损伤值,并记录累积损伤失效时的步长设计方案。均分法设计的步长划分见表10,试验剖面见图23。
Table 10 Divided profile step size of the averaging method

表10 均分法剖面步长划分

步进顺序 振动载荷/Grms 各级载荷下的损伤 合计损伤值
1 2 1.613×10-7 0.578
2 4 1.018×10-5
3 6 0.000110
4 8 0.000640
5 10 0.00243
6 12 0.00725
7 14 0.0182
8 16 0.0405
9 18 0.0820
10 20 0.154
11 22 0.272
12 24 0.458 1.036
Fig.23 Experimental profile designed using the averaging method

图23 均分法设计的试验剖面图

Full size|PPT slide

同理,将均分法设计的振动试验剖面作为试验输入激励,进行x轴向的振动HALT试验。将产品置于20Grms量级的载荷下振动10min,测试输出信号,见图24(a),示波器采集到的信号与该产品非振动下的输出信号一致,产品模块功能正常。将振动量级调至22Grms,示波器采集到前、主级两级延时时间为692.0μs的输出信号,见图24(b),该延时时间在合格范围内,因此产品模块功能正常。将振动量级调至24Grms,通电测试其输出信号,示波器无信号,无法实现正常放电,见图24(c),该产品模块功能故障,恢复到上一级振动应力继续试验,功能仍然异常,停止试验。
Fig.24 Discharge curve of vibration HALT test fuse under the uniform distribution method profile

图24 均分法剖面下的振动HALT试验引信放电曲线

Full size|PPT slide

产品x轴向试验振动载荷量级与测试结果见表11,确定产品模块的振动破坏极限在22~24Grms之间。
Table 11 Vibration load and test results of the equal distribution method test

表11 均分法试验振动载荷与测试结果

步进顺序 试验振动载荷/Grms 步长/Grms 测试结果
1 2 2 正常
2 4 2 正常
3 6 2 正常
4 8 2 正常
5 10 2 正常
6 12 2 正常
7 14 2 正常
8 16 2 正常
9 18 2 正常
10 20 2 正常
11 22 2 正常
12 24 2 异常
13 22 -2 异常
停止试验后,解除引信保护结构,观察产品故障部位,由图25所示,产品电路模块中的大陶瓷电阻管脚发生断裂,故障部位与图12仿真结果、图19反馈近似损伤法及图22标准固步法试验结果一致。综合上述均分法仿真及试验结果,均分法步进次数为12次,试验时间为12次×10min=120min,故障部位为大陶瓷电阻,破坏极限区间为[24Grms]。
Fig.25 Cracks in the pins of large ceramic resistors caused by vibration testing using the equal distribution method

图25 均分法振动试验引起大陶瓷电阻管脚裂纹

Full size|PPT slide

利用仿真及试验对3种剖面步长制定方法进行对比,见表12及图26。
Table 12 Comparison of step size division methods

表12 步长划分方法对比

序号 方法 步长/Grms 破坏极限区间/Grms 激发精度对比 总时间/min 总时间对比 故障部位
1 反馈近似损伤法 5;2.35;2 [23.35,25.35] 80 大陶瓷电阻
2 标准固步法 5 [25,30] 1对比2:60% 60 1对比2:-33% 大陶瓷电阻
3 均分法 2 [22,24] 1对比3:0 120 1对比3:33% 大陶瓷电阻
Fig.26 Profile step curves of three methods

图26 3种方法剖面步长曲线

Full size|PPT slide

标准固步法以5Grms的大步长逐级施加,虽步进次数较少,总步进试验时间较短,但其预测破坏极限的激发精度较低,仅能确定在[30Grms]的5Grms范围内;均分法以2Grms的小步长逐级施加,虽激发精度较高,可确定在2Grms的范围内,但其步进次数较多,总步进试验时间较长;反馈近似损伤法设计的剖面步长采用了变步长的方法,先以5Grms大步长快速步进,再以2.35Grms的步长过渡,最后以2Grms的小步长逼近破坏极限。方法对比优势如下:
1)相对于5Grms激发精度、60min总步进时间的标准固步法,反馈近似损伤法80min的总步进时间虽略大标准固步法33.33%,但破坏极限激发精度由5Grms提升至2Grms,提升了60%。
2)相对于2Grms激发精度、120min总步进时间的均分法,反馈近似损伤法在保证2Grms的高破坏极限激发精度的基础上,将总试验时间缩短至80min,缩短了33.33%,降低了试验成本。
反馈近似损伤法以每步损伤增量近似为约束,逐步迭代各级步长,所设计的试验剖面前期步长大加快试验进程,试验后期步长小提高试验破坏极限激发精度,中期每步损伤增量相等实现步长由大到小合理量化过渡。

5 结论

为打通机电产品振动HALT试验设计中累积损伤与关键要素之间的定量关联机制,本文提出一种基于反馈近似损伤的振动加速激励设计方法,结合振动损伤机制分析与功率谱密度频域解析技术建立了CM-VED,以某型引信为案例,通过试验验证方法的有效性。得出以下主要结论:
1)为量化振动激励与累积损伤之间的映射关系,结合振动损伤机制分析与功率谱密度频域解析技术建立了CM-VED,以某航天精密机电组件高加速振动步进数据验证模型有效性,结果表明,最大对比误差Er,max=2.15%,平均对比误差 Er¯=0.672%。
2)为精准实现损伤数据与试验剖面之间的转换,基于CM-VED,利用迭代反馈控制策略,以每步损伤增量近似为约束,以高加速寿命试验标准指南规定的步长增量范围为限制条件,提出了基于反馈近似损伤的振动加速激励设计方法,精确调控每一振动步骤中的损伤增量,从而实现对振动载荷的逐步精确控制。
3)以某型引信为案例,采用基于反馈近似损伤的振动加速激励设计方法设计的剖面进行振动试验,结果表明,依据所提方法仿真计算得出的产品破坏极限及故障模式,与实际试验的结果吻合。与标准固步法及均分法进行对比,所提方法较标准固步法激发精度提升60%,较均分法在保证高激发精度的基础上时间缩短33.33%。
4)基于反馈近似损伤的振动加速激励设计方法可进一步应用于机电产品的振动HALT试验剖面设计,通过定位产品的故障模式,建立薄弱环节的CM-VED,进而采用基于反馈近似损伤的振动加速激励设计方法设计适用于产品的试验剖面。

References

Publishing order | Descend order by publishing year | Descend order by cited within
[1]
WANG Y J, KANG R, CHEN Y. Reliability assessment of engine electronic controllers based on Bayesian deep learning and cloud computing[J]. Chinese Journal of Aeronautics, 2021, 34(1):252-265.
Cited in this article [1]
[2]
魏冰阳, 郭玉梁, 古德万, 等. 弧齿锥齿轮弯曲疲劳寿命仿真与加速试验评价[J]. 兵工学报, 2022, 43(11):2945-2952.
https://doi.org/10.12382/bgxb.2021.0601
Abstract
疲劳寿命试验是齿轮强度评价必不可少的手段，但长期以来弧齿锥齿轮疲劳试验数据缺乏，导致相关产品设计存在较大的不确定性。本文建立了弧齿锥齿轮三维有限元模型，给出了相应的弯曲疲劳寿命仿真计算流程；探讨了加速疲劳试验的机理与方法，确定了加速疲劳试验应力因子。对20CrNiMo材料试棒进行了拉伸疲劳强度试验，获得了材料的S-N曲线，以此为基础数据，利用三维有限元软件完成了两个水平的弯曲疲劳寿命仿真计算；在专用闭功率流耐久性试验台上进行了若干组齿轮的弯曲强度疲劳寿命试验，疲劳寿命与理论仿真结果对比误差小于3.2%，一致性较好。证明了以疲劳寿命仿真与加速试验手段评价复杂结构件锥齿轮弯曲疲劳强度的可行性。
WEI B Y, GUO Y L, GU D W, et al. Evaluation of bending fatigue life of spiral bevel gears by simulation and accelerated test[J]. Acta Armamentarii, 2022, 43(11):2945-2952. (in Chinese)
https://doi.org/10.12382/bgxb.2021.0601
Cited in this article [1] Abstract
Fatigue life testing is an indispensable method for evaluating the gear strength of spiral bevel gears, but the lack of fatigue test data has long led to high uncertainties in the design of related products. This study establishes a three-dimensional finite element model for a spiral bevel gear and presents a simulation calculation of the corresponding bending fatigue life. The mechanism and methods of the accelerated fatigue test are discussed, and the stress factors for the accelerated test are presented. The tensile fatigue strength test is carried out on the 20CrNiMo material test bar, and the S-N curve of the material is obtained. Based on this, a three-dimensional finite element software is used to complete multiple calculations of simulated digital bending fatigue life in a special closed power flow bevel gear. The durability test bench has been used to conduct several sets of tests on gear bending strength and fatigue life. Test results and theoretical simulation results are in good agreement, with a comparison error of less than 3.2%. Through fatigue life simulation and accelerated testing, the feasibility of the evaluation method is proved. The approach works well in evaluating the bending fatigue strength of bevel gears with complex structures.
[3]
KAROL K, MINA T. Failure mode and reliability study for electrical facility of the high temperature engineering test reactor[J]. Reliability Engineering and System Safety, 2021, 210(3):107529.
Cited in this article [1]
[4]
赵晓东, 穆希辉. 加速度计贮存试验及寿命评估方法研究[J]. 兵工学报, 2020, 41(6):1227-1235.
https://doi.org/10.3969/j.issn.1000-1093.2020.06.020
Abstract
针对长期贮存后加速度计寿命难以评估的问题，提出一种综合利用加速试验数据与自然贮存试验数据的评估方法。采用极小卡方估计和拟合优度检验，处理加速度计的自然贮存数据，得到其可能服从的4种寿命分布函数，确定加速度计寿命分布形式为威布尔分布和Ⅰ型极大值分布；基于加速度计的先验信息，设计并开展加速度计的步进加速寿命试验，获得加速度计的加速失效数据；在威布尔分布和I型极大值分布假设下，依据加速失效数据估计加速度计寿命分布模型参数，采取加速因子变异系数的方法，选定Ⅰ型极大值分布为加速度计的寿命分布函数，得出常规应力水平下可靠度0.90和0.95的寿命分别为14.917 6 a和10.052 4 a. 通过对比标准贮存环境中和寿命分布模型中加速度计的失效比率，验证了综合利用两种试验数据评估加速度计寿命方法的有效性。
ZHAO X D, MU X H. Storage life evaluation of accelerometer based on accelerator factor coefficient of variation[J]. Acta Armamentarii, 2020, 41(6):1227-1235. (in Chinese)
https://doi.org/10.3969/j.issn.1000-1093.2020.06.020
Cited in this article [1] Abstract
Aiming at the problem that the life of accelerometers is difficult to evaluate after long-term storage, an evaluation method that comprehensively uses accelerated test data and natural storage test data was proposed. The minimum Chi-square estimation and goodness-of-fit test was used, the accelerometer's natural storage data was processed to obtain the four life distribution functions that it may obey, and the accelerometer life distribution was determined as Weibull distribution and type Ⅰ maximum distribution; With reference to the a priori information of the accelerometer, a step-by-step acceleration life test of the accelerometer is designed and carried out to obtain acceleration failure data of the accelerometer; under the assumptions of Weibull distribution and type Ⅰ maximum value distribution, the parameters of the accelerometer life distribution model are estimated based on accelerated failure data, and the method of acceleration factor variation coefficient is used to select the type Ⅰ maximum value distribution as the life distribution function of the accelerometer. The lifespan of reliability 0.90 and 0.95 under conventional stress level is 14.917 6 a and 10.052 4 a, respectively. By comparing the failure rate of accelerometers in the standard storage environment and the life distribution model, the effectiveness of using two test data to evaluate the lifespan of the accelerometer is verified. Key
[5]
WANG, J Y, LIU Z, WANG J H, et al. A general enhancement method for test strategy generation for the sequential fault diagnosis of complex systems[J]. Reliability engineering & system safety, 2022, 228(12):108754.
Cited in this article [1]
[6]
LIU F C, WEI P F, ZHOU C C, et al. Reliability and reliability sensitivity analysis of structure by combining adaptive linked importance sampling and Kriging reliability method[J]. Chinese Journal of aeronautics, 2020, 33(4):1218-1227.
Cited in this article [2]
[7]
孙树磊, 雷丽妃, 黄海波, 等. 基于用户作业工况的履带式挖掘机加速疲劳强化路面构建方法[J]. 机械工程学报, 2022, 58(16):319-328.
https://doi.org/10.3901/JME.2022.16.319
Abstract
为提高挖掘机疲劳强度安全可靠性，解决挖掘机用户作业工况及加速疲劳试验方法缺乏等问题，以挖掘机油箱为研究对象，基于等效损伤原则，通过用户工况调研、采石场试验测试、虚拟路面构建、多体动力学仿真、强化路面试验验证及疲劳损伤计算等一系列流程，提出一种基于挖掘机用户作业工况的履带式挖掘机加速疲劳强化路面构建方法。结果表明，采用爬碎石坡等共9种采石场试验测试工况表征用户作业工况，可获得量化的工况测试数据及目标总损伤；基于多体动力学构建的挖掘机动力学仿真模型及虚拟强化路面计算结果与真实强化路面试验测试结果较为吻合；基于该方法获得了与目标总损伤一致的多种不同的强化路面及不同档位速度组合工况，其中由0.3 m凸块间距1档、2 m凸块间距1档及15 m凸块间距1档3种工况所构成的强化路面组合工况较优，强化系数为15.1，该方法可大幅度降低挖掘机整机及关键零部件的疲劳试验时间。
SUN S L, LEI L F, HUANG H B, et al. Construction method for accelerated fatigue reinforced pavement of crawler excavator based on user operating conditions[J]. Journal of Mechanical Engineering, 2022, 58(16):319-328. (in Chinese)
https://doi.org/10.3901/JME.2022.16.319
Cited in this article [1] Abstract
In order to improve the fatigue strength safety and reliability of excavators, and solve the problems of the lack of the excavator user operating conditions and accelerated fatigue test methods, a construction method for accelerated fatigue reinforced pavement of crawler excavator based on user operating conditions is proposed with the excavator fuel tank as the research object, through a series of processes such as user condition investigation, quarry test, virtual pavement construction, multi-body dynamics simulation, reinforced pavement test verification and fatigue damage calculation. The results show that: 9 quarry test conditions including climbing gravel slopes, and the quantified test data and target total damage are obtained. The excavator dynamics simulation model constructed based on multi-body dynamics and the calculation results of the virtual reinforced pavement are more consistent with the test results of the real enhanced pavement. Based on this method, a variety of different reinforced pavements and different gear speed combinations consistent with the target total damage are obtained. The operating condition composed of bumps interval 0.3 m and gear 1, bumps interval 2 m and gear 1, and bumps interval 15 m and gear 1 is better, and the intensified coefficient is 15.1. This method can be used for greatly reducing fatigue test time of the excavator and the key parts.
[8]
MUGNAINI M, ADDABBO T, FORT A, et al. Magnetic brakes material characterization under accelerated testing conditions[J]. Reliability engineering & system safety, 2020, 193(1):106614.
Cited in this article [1]
[9]
HAO P, YANG H, WANG Y T, et al. Efficient reliability-based design optimization of composite structures via isogeometric analysis[J]. Reliability engineering & system safety, 2021, 209(5):107465.
Cited in this article [1]
[10]
WU Q F, WANG M Q, ZHOU W Y, et al. Traction inverter highly accelerated life testing with High-Temperature stress[J]. IEEE Transactions on Transportation Electrification, 2021, 7(1):304-316.
Cited in this article [2]
[11]
HUANG J L, GOLUBOVIC D S, KOH S, et al. Lumen degradation modeling of white-light LEDs in step stress accelerated degradation test[J]. Reliability engineering & system safety, 2016, 154(10):152-159.
Cited in this article [1]
[12]
REFAEY R M. Estimating and prediction accelerated life test using constant stress for Marshall-Olkin extended burr Type X distribution based on Type-II censoring[J]. Al-Azhar Bulletin of Science, 2021, 32(1):45-59.
Cited in this article [2]
[13]
薛小锋, 徐光铎, 冯蕴雯, 等. 基于元件降额设计的温度步进强化试验剖面设计[J]. 系统工程与电子技术, 2023, 45(12):4073-4083.
https://doi.org/10.12305/j.issn.1001-506X.2023.12.38
Abstract
针对目前强化试验剖面效率低、成本高的问题, 提出了某型弹类电子产品温度强化试验剖面设计框架。结合产品可靠性框图对试验对象进行失效逻辑分析, 基于元器件降额的步长设计方法(step design method based on component derating, CD-SDM)优化步长、缩短试验时间, 采用基于有限元仿真的确定性分析方法获得工作极限和破坏极限估值, 降低步长划分时极限间工作裕度的影响, 实现步长、试验时间和其他要素的优化。以某型弹类电子产品高温步进为例验证所提方法, 结果表明获得的温度强化试验剖面较传统方法在试验时间上最少可缩短13.33%左右, 与传统方法相比减少了1/4的检测次数, 优化了目前可靠性强化试验剖面设计对弹类电子产品试验效率低、成本高的问题。
XUE X F, XU G D, FENG Y W, et al. Temperature enhancement test profile design for a bullet electronics based on component derating[J]. Systems Engineering and Electronics, 2023, 45(12):4073-4083. (in Chinese)
Cited in this article [1]
[14]
姬亚萌, 张卫正, 原彦鹏, 等. 高强化柴油机活塞加速热疲劳与等效寿命评估方法[J]. 兵工学报, 2022, 43(12):3008-3019.
JI Y M, ZHANG W Z, YUAN Y P, et al. Study of equivalent and influence laws of accelerated thermal fatigue life of aluminum alloy pistons in highly strengthened diesel engines[J]. Acta Armamentarii, 2022, 43(12):3008-3019. (in Chinese)
Cited in this article [1]
[15]
JAKOB F, KIMMELMANN M, BERTSCHE B. Selection of acceleration models for test planning and model usage[J]. IEEE Transactions on Reliability, 2017, 66(2):298-308.
Cited in this article [1]
[16]
KIM S K, KIM Y S, SUNG S. Practical design of partially accelerated degradation test with two stress variables under step-stress loading scheme[J]. Microelectronics Reliability, 2023, 150(11),109-115.
Cited in this article [1]
[17]
TAO J, YU Z Y, REN Z Q, et al. Study of an adaptive accelerated model and a data transfer method based on a reliability enhancement test[J]. Eksploatacja i Niezawodno ść, 2014, 16(1):128-132.
Cited in this article [3]
[18]
ALEX F D, PRAKASH O Y, VAL M. A review of methods for the reliability testing of flexible hybrid electronics[J]. IEEE Transactions on Components,Packaging and Manufacturing Technology, 2020, 10(11):1902-1912.
Cited in this article [1]
[19]
HAN D, BAI T Y. Parameter estimation using EM algorithm for lifetimes from step-stress and constant-stress accelerated life tests with interval monitoring[J]. IEEE Transactions on Reliability, 2021, 70(1):49-64.
Cited in this article [3]
[20]
LING M H, HU X W. Optimal design of simple step-stress accelerated life tests for one-shot devices under Weibull distributions[J]. Reliability Engineering & System Safety, 2020, 193:106630.
Cited in this article [3]
[21]
YAN W A, XU X F, BIGAUD D, et al. Optimal design of step-stress accelerated degradation tests based on the Tweedie exponential dispersion process[J]. Reliability Engineering & System Safety, 2023, 230:108917.
Cited in this article [3]
[22]
ZHANG J Q, KONG X W, LI X Y, et al. Fault diagnosis of bearings based on deep separable convolutional neural network and spatial dropout[J]. Chinese Journal of Aeronautics, 2022, 35(10):301-312.
Cited in this article [3]
[23]
WANG Z H, LIU G, LI W B, et al. A novel optimal accelerated degradation test design method considering multiple decision variables[J]. Microelectronics Reliability, 2021, 124:114334.
Cited in this article [3]
[24]
CZERNY B, KHATIBI G. Highly accelerated lifetime testing in power electronics[C]// Proceedings of the 54th International Symposium on Microelectronics. San Diego,CA, US: International Microelectronics Assembly and Packaging Society, 2021:390-396.
Cited in this article [2]
[25]
郭伟超, 赵怀山, 李成, 等. 基于小波包能量谱与主成分分析的轴承故障特征增强诊断方法[J]. 兵工学报, 2019, 40(11):2370-2377.
https://doi.org/10.3969/j.issn.1000-1093.2019.11.022
Abstract
滚动轴承出现损伤时，采集的振动信号呈非平稳性，采用一般的时域和频域分析方法不能准确提取出振动信号的故障特征。根据小波包多分辨、精细化的分解特性，提出一种基于小波包能量谱与主成分分析（PCA）方法的滚动轴承故障诊断算法。将振动信号进行小波包分解，得到重点频率段信息的能量谱，提取能量谱作为特征向量；利用PCA方法对特征向量降维并减小噪声信号的干扰，获得增强的故障特征；利用层次聚类方法和改进的模糊c均值聚类算法对不同类型的滚动轴承故障进行识别，两种聚类方法都准确地识别出了不同的故障类型。实例验证结果表明，所提方法能够有效地提取振动信号中的有用故障特征，实现轴承故障类型的精确诊断。
GUO W C, ZHAO H S, LI C, et al. Fault feature enhancement method for rolling bearing fault diagnosis based on wavelet packet energy spectrum and principal component analysis[J]. Acta Armamentarii, 2019, 40(11):2370-2377. (in Chinese)
Cited in this article [1]
[26]
LIU J, DONG X Z, WANG X W, et al. A homogenization-planning-tracking method to solve cooperative autonomous motion control for heterogeneous carrier dispatch systems[J]. Chinese Journal of Aeronautics, 2022, 35(9):293-305.
Cited in this article [1]
[27]
杨彦彰, 朱建华, 张华, 等. 电工电子产品加速应力试验规程高加速寿命试验导则:GB/T 29309—2012[S]. 北京: 工业和信息化部, 2012.
YANG Y Z, ZHU J H, ZHANG H, et al. Accelerated stress testing code for electrical and electronic products-Guidelines for high acceleration life testing:GB/T 29309—2012[S]. Beijing: Ministry of Industry and Information Technology, 2012. (in Chinese)
Cited in this article [8]
[28]
RAHE D, DRAKE, DOERTENBACH N. Qualmark HALT testing guidelines:933-0336[S]. Denver,CO,US: Qualmark Corporation, 2020.
Cited in this article [8]
[29]
程祥利, 刘波, 赵慧. 侵彻战斗部-引信系统动力学建模与仿真[J]. 兵工学报, 2020, 41(4):625-633.
https://doi.org/10.3969/j.issn.1000-1093.2020.04.001
Abstract
为揭示侵彻过程中引信电路模块的动态响应机理，将机械振动理论引入侵彻过程理论分析与计算，提出一种简化的侵彻战斗部-引信系统动力学模型。以侵彻战斗部-引信系统的载荷传递关系为基础，基于多自由度弹簧-质量-阻尼系统建立模型的动力学微分方程；通过谐响应分析确定固有频率、阻尼比等动力学参数，并采用数值积分的方法预测不同侵彻工况下的响应特性；从系统幅频响应特性的角度分析响应特性与传统经验公式解有很大差异的原因。与谐响应分析结果、火炮试验实测过载信号的对比分析表明：提出的动力学模型能准确、快速地预测战斗部、引信在侵彻过程中的响应特性；考虑轴向振动后，侵彻战斗部表现出明显的振动放大特性与周期振荡特性，而且是影响引信电路模块响应特性的首要因素。
CHENG X L, LIU B, ZHAO H, et al. Dynamic modeling and simulation for penetration warhead-fuze system[J]. Acta Armamentarii, 2020, 41(4):625-633. (in Chinese)
https://doi.org/10.3969/j.issn.1000-1093.2020.04.001
Cited in this article [1] Abstract
The mechanical vibration theory is introduced into theoretical analysis and calculation of penetration process, and a simplified dynamic model of penetration warhead-fuze system is proposed with the purpose of revealing the dynamic response mechanism of circuit module of fuze in penetration process. On the basis of analysis of loading transfer relation, a dynamic differential equation is established based on multi-DOFs spring-mass-damper system, and the dynamic parameters, such as natural frequency and damping ratio, are determined by the harmonic response analysis. Then the dynamic characteristics under different penetration conditions are predicted by numerical integration method, and the reason why the predicted dynamic characteristics differ greatly from the calculated result of the traditional empirical formula is analyzed from the amplitude-frequency response.The credibility of the proposed model was verified through artillery test, and the overload signal in penetration process was collected. The calculated value of overload signal is in agreement well with measured result. The result shows that the proposed model is more suitable to predict the dynamic characteristics of warhead or fuze in penetration process. It is shown that penetration warhead exhibits obvious vibration amplificatory characteristics and periodic oscillation characteristics in considering the axial vibration effect, and the dynamic characteristics of warhead are the most important factor affecting the dynamic characteristics of circuit module in fuze.Key
[30]
邱士起. 冲击作用下引信起爆控制系统关键元器件失效机理及其可靠性分析[D]. 北京: 北京理工大学, 2016:53-68.
QIU S Q. Failure mechanism of key components of fuze detonation control system under impact action and its reliability analysis[D]. Beijing: Beijing Institute of Technology, 2016:53-68. (in Chinese)
Cited in this article [1]
[31]
SHARP A, ANDRADE J, RUFFINI N. Design for reliability for the high reliability fuse[J]. Reliability Engineering & System Safety, 2019, 181:54-61.
Cited in this article [1]
[32]
ZHANG D Q, CHEN Y Y. Random vibration fatigue life analysis of airborne electrical control box[J]. Applied Sciences, 2022; 12(14):7335-7335.
Cited in this article [1]
[33]
杨硕, 杜天玮, 张晓鹏, 等. 外物损伤对叶片振动疲劳裂纹扩展性能的影响[J]. 兵工学报, 2023, 44(6):1713-1721.
YANG S, DU T W, ZHANG X P, et al. Effect of foreign object damage on vibration fatigue crack propagation of blades[J]. Acta Armamentarii, 2023, 44(6):1713-1721. (in Chinese)
https://doi.org/10.12382/bgxb.2022.0109
Cited in this article [1] Abstract

In order to study the effect of foreign object damage (FOD) on the fatigue crack propagation of aero-engine blades, using the drop weight impact testing equipment, the FOD simulation test and vibration fatigue test of TC4 titanium alloy specimens were carried out under different impact energies. The relationship between the crack length and fatigue life of the damaged specimens was obtained, and the parameters of fatigue fracture crack morphology were fitted to establish a fatigue crack growth prediction and calculation model. The results showed that: The depth and width of the notch decreased nonlinearly with the decrease of impact energy; when the impact energy is large, the fatigue crack propagates first along the bending microcrack and then along the straight line; when the impact energy is small, the fatigue crack of the specimen keeps linear propagation; the crack initiation life is related to both impact energy and stress level.
[34]
WANG L J, WANG Z W. FEM verification of accelerated vibration test method based on Grms-T curve[J]. Advances in Mechanical Engineering, 2022, 14(2):1-12.
Cited in this article [1]
[35]
马岩. 航天精密机电组件高加速筛选试验模拟与仿真[D]. 西安: 西安电子科技大学, 2016:28-32.
MA Y. Highly accelerated stress screen modeling and simulation of aerospace precision electromechanical component[D]. Xi'an: Xidian University, 2016:28-32. (in Chinese)
Cited in this article [1]
[36]
徐保荣, 王涛, 梁梓. 基于操纵动作预测的履带车辆载荷谱编制方法与流程[J]. 兵工学报, 2022, 43(2):252-259.
XU B R, WANG T, LIANG Z. Generating method and process of load spectra for tracked vehicles based on prediction of manipulating action[J]. Acta Armamentarii, 2022, 43(2):252-259. (in Chinese)
https://doi.org/10.3969/j.issn.1000-1093.2022.02.002
Cited in this article [1] Abstract
A new generating method of load spectrum for tracked vehicles is proposed based on load spectrum blocks and training subjects to cope with the problem of insufficient sample size. Action of vehicles and driving behavior are predicted by using path planning algorithm and action planning algorithm. Training subjects and geographic information are used as input data, the predicted vehicle situation and driving behavior are taken as indexes to get load spectrum blocks, and the time domain load spectrum are generated by spliced load spectrum blocks. The verification test results show that the load data samples generated by splicing method can reflect the vehicle working conditions correctly, and it can be used to generate load samples rapidly.
PDF(15182 KB)

4

Accesses

0

Citation

Detail
Sections
Recommended

/

〈 〉