PDF(7646 KB)
A CNN-SVM-based Adapter Drop Point Prediction Algorithm
SUZhengyu, YANGBaosheng, YANGJing, TANGJingnan, JIANGYi, DENGYueguang
PDF(7646 KB)
Sponsored by: China Association for Science and Technology (CAST)
Editor-In-Chief: Xu Yida
ISSN 1000-1093
Hosted By: China Ordnance Society
Published By: Acta Armamentarii
CN 11-2176/TJ
PDF(7646 KB)
A CNN-SVM-based Adapter Drop Point Prediction Algorithm
To address the prolonged processing and resource consumption challenges in the launch process adapter drop point prediction algorithm,a adapter drop point prediction model with convolutional neural network and support vector machine (CNN-SVM) is proposed.The adapter dynamics and motion models are established by utilizing Euler angle representation,and the fourth-order Runge-Kutta method is used to numerically solve the motion trajectory of adapter to provide the extensive motion state parameters and drop point information.The CNN-SVM-based adapter drop point prediction model uses the Adam optimizer to optimize CNN network performance,and determines optimal SVM hyperparameters through mesh searching.Simulated results show that the proposed model has high solution accuracy and robust generalization performance for adapter drop prediction,achieving R2 values exceeding 0.99 for both training and test sets and the mean absolute error (MAE) less than 0.1m.The solution time of the proposed method is only 8.5% compared to that of the traditional numerical integration method under the conditions of equivalent resources and the required prediction accuracy.The proposed model offers an efficient solution for rapidly predicting the adapter separation drop point during the launch process.
drop point prediction / adapter / convolutional neural network / support vector machine {{custom_keyword}} /
Table 1 CNN model structural parameters表1 CNN模型结构参数 |
| 结构 | 卷积核 | 特征数 | 输出尺寸 |
|---|---|---|---|
| 输入层 | 7×1×1 | ||
| 卷积层1 | 2×1 | 32 | 6×1×32 |
| 池化层1 | 2×1 | 32 | 3×1×32 |
| 卷积层2 | 2×1 | 64 | 2×1×64 |
| 池化层2 | 2×1 | 64 | 1×1×64 |
| 全连接层 | 2×1×192 |
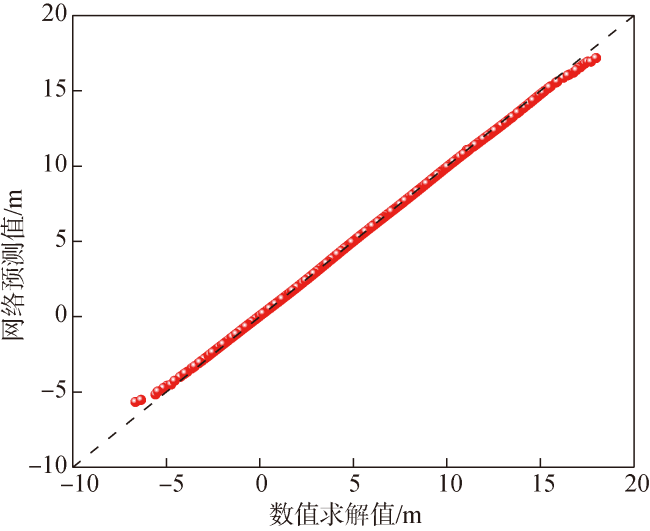
Fig.11 Predicted results of X-direction training set (R2=0.9968)图11 X轴方向训练集预测结果(R2=0.9968) |
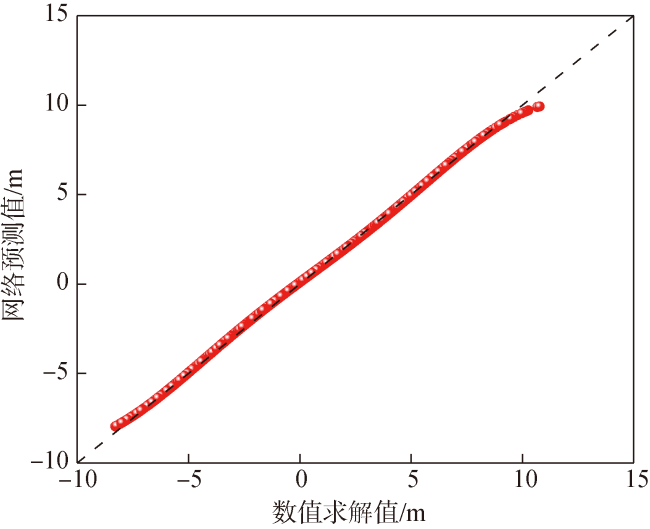
Fig.12 Predicted results of Y-direction training set (R2=0.9977)图12 Y轴方向训练集预测结果(R2=0.9977) |
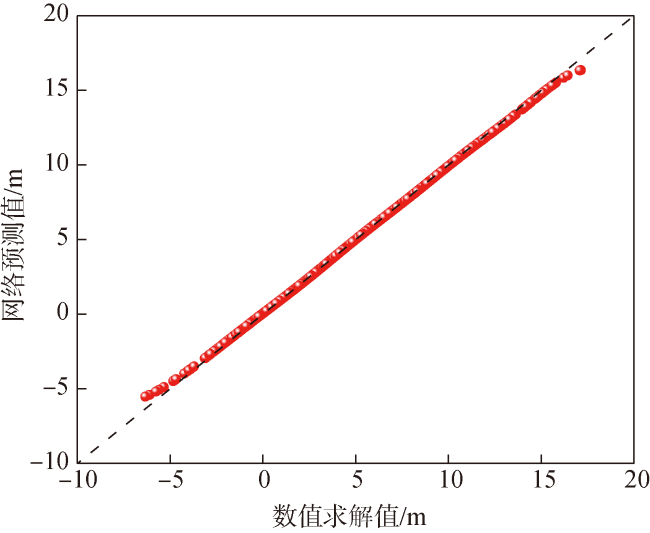
Fig.14 Predicted results of X-direction training set (R2=0.9972)图14 X轴方向测试集预测结果(R2=0.9972) |
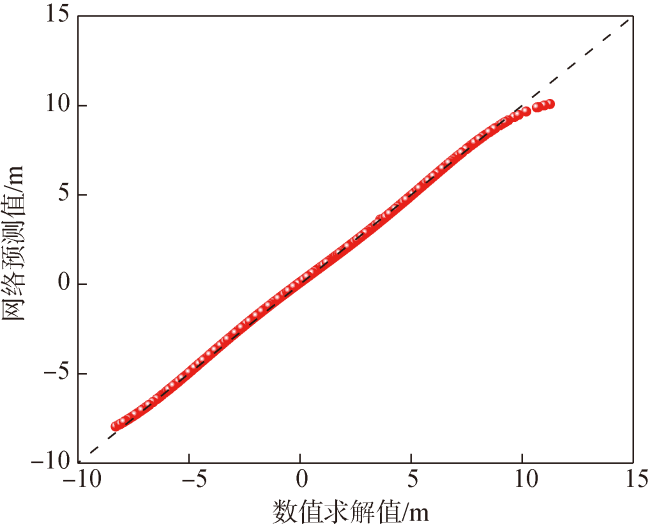
Fig.15 Predicted results of Y-direction training set (R2=0.9973)图15 Y轴方向测试集预测结果(R2=0.9973) |
Table 2 Initial conditions for Monte Carlo experiment表2 蒙特卡洛实验初始条件 |
| 参数 | 数值 |
|---|---|
| 初始X轴方向分离速度/(m·s-1) | (3,3) |
| 初始Y轴方向分离速度/(m·s-1) | (-3,3) |
| 初始Z轴方向分离速度/(m·s-1) | (0,40) |
| 初始分离角速度/(rad·s-1) | (-15,15) |
| 外部X轴方向风速/(m·s-1) | (-10,10) |
| 外部Y轴方向风速/(m·s-1) | (-10,10) |
| 发射过程随机振动/dB | (-5,5) |
| [1] |
姜毅, 魏昕林, 陈苗. 发射动力学[M]. 北京: 北京理工大学出版社, 2015.
{{custom_citation.content}}
{{custom_citation.annotation}}
|
| [2] |
岳松堂, 李艳琨, 李永彬. 美国陆军防空反导装备最新发展态势分析及启示[J]. 现代军事, 2016(8):49-56.
{{custom_citation.content}}
{{custom_citation.annotation}}
|
| [3] |
张英琦, 乐贵高, 马大为, 等. 适配器与收缩段对同心筒发射流场的影响[J]. 北京理工大学学报, 2018, 38(6):557-564.
{{custom_citation.content}}
{{custom_citation.annotation}}
|
| [4] |
陶倩楠, 姜毅, 史少岩, 等. 导弹适配器数值模拟风洞试验[J]. 飞行力学, 2017, 35(5):92-96.
{{custom_citation.content}}
{{custom_citation.annotation}}
|
| [5] |
岳玉娜, 郝继光, 吴艳. 导弹适配器分离过程虚拟试验研究[J]. 兵器装备工程学报, 2018, 39(7):71-75. (in Chinese)
{{custom_citation.content}}
{{custom_citation.annotation}}
|
| [6] |
刘冰, 程栋, 卢丙举, 等. 含适配器的潜射导弹运载器跨介质发射分离建模与仿真[J]. 兵工学报, 2023, 44(5):1237-1250.
In order to solve the problem of transmedia ejection separation of missile carrier with elastic adapter, based on the fractional areas-volume obstacle representation (FAVOUR) method, a multi-physical field coupling model for missile separation from the carrier near the free surface is established by using the RNG k-ε turbulence model and VOF function. The numerical simulation of the water entry process of the cylinder is carried out, and the calculated results are consistent with the experimental data, which verifies the rationality of the numerical model. The ejection and separation processes of the missile in trough and crest environments and at different initial pitch angles and initial velocities of water exit are numerically simulated, and the effects of initial pitch angle, water exit velocity and position above the water surface on the submarine-launched missile separated from the carrier are obtained. Considering the pitch angle of the missile at the moment of separation from the launch tube at the wave crest and trough positions, the optimal initial pitch angle is 3.24° based on the criterion that the pitch angle of the missile reaches 0° at the separation time at the wave trough position. The simulation method and results are of referential significance for engineering applications.
{{custom_citation.content}}
{{custom_citation.annotation}}
|
| [7] |
张子豪, 王汉平. 考虑弹-筒柔性的潜载导弹弹射多体动力学分析方法[J]. 兵工学报, 2022, 43(2):305-315.
在潜载导弹垂直弹射过程中，导弹的姿态变化是关系其发射成败的关键。针对潜载导弹垂直弹射过程提出一种可同时考虑弹体和发射筒柔性的弹射发射动力学建模分析方法。运用改进的柔性点线高副模型来模拟适配器的抗压和抗弯载荷，基于弹体水动力、附连水惯性力的单元线性分布假设，利用Hermite形状函数将单元分布载荷等效简化为单元节点集中力，并编程实现加载。仿真结果表明：导弹姿态与实验数据吻合较好，验证了该分析方法可信、实用；该方法为同时考虑导弹弹体-发射筒柔性的潜射动力学建模提供了新思路，也为拓展柔性体之间接触的简化建模提供了新途径。
{{custom_citation.content}}
{{custom_citation.annotation}}
|
| [8] |
周晓和, 刘伟, 张家骏, 等. 动平台飞行器发射动力学及适配器影响研究[J]. 战术导弹技术, 2023(4):119-125.
{{custom_citation.content}}
{{custom_citation.annotation}}
|
| [9] |
{{custom_citation.content}}
{{custom_citation.annotation}}
|
| [10] |
{{custom_citation.content}}
{{custom_citation.annotation}}
|
| [11] |
任济寰, 吴祥, 薄煜明, 等. 基于增强上下文信息长短期记忆网络的弹道轨迹预测[J]. 兵工学报, 2023, 44(2):462-471.
根据己方观测数据进行弹道轨迹预测是现代陆军实施精准打击的重要一环。针对现有弹道轨迹预测方法存在精度不足且实时性不强的问题,提出一种新的增强上下文信息长短期记忆(CE-LSTM)网络轨迹预测模型,进行弹道轨迹的长期精准预测。在LSTM网络可逼近任意非线性函数且具备长期记忆能力的基础上,构建隐藏层输出混合单元提取短时上下文信息,进一步逼近弹体运动状态;通过建立不同条件下的弹道轨迹的数据集,训练得到具备最优超参数的CE-LSTM网络。实验结果表明,与弹道微分方程组的数值积分解法以及高斯混合模型相比,CE-LSTM网络在预测的精度上优于其他2种方法,预测速度提高了3~10倍,且具备较强的泛化能力。
Trajectory prediction based on observed data is critical to the modern army's precision strike capability. Yet, the existing trajectory prediction methods have suffer from low accuracy and poor real-time performance. Thus, this study proposes a new model called Context-enhanced Long Short-Term Memory(CE-LSTM) Network to make an accurate long-term prediction of the exterior trajectory of incoming projectiles. The proposed method inherits the LSTM network's advantage in that it can approximate any nonlinear function and it has a long-term memory. Furthermore, we create a mixture output unit of the hidden layer to extract short-term context information and approximate the motion states of the incoming projectiles more accurately. The CE-LSTM network is trained with a large-scale dataset consisting of exterior trajectories under different initial conditions to obtain the optimal hyper-parameters. The experimental results show that compared with the methods like external ballistic differential equations and the Gaussian mixture model, the CE-LSTM network performs significantly better in prediction accuracy, and its prediction speed increases by three to ten times. Moreover, the proposed method is highly generalizable. {{custom_citation.content}}
{{custom_citation.annotation}}
|
| [12] |
{{custom_citation.content}}
{{custom_citation.annotation}}
|
| [13] |
郑志伟, 管雪元, 傅健, 等. 基于卷积神经网络与长短期记忆神经网络的弹丸轨迹预测[J]. 兵工学报, 2023, 44(10) :2975-2983.
针对弹丸非线性轨迹预测问题,提出一种基于卷积神经网络(CNN)与长短期记忆(LSTM)神经网络的混合轨迹预测模型。通过建立6自由度弹丸运动模型,并使用4阶龙格库塔法外弹道仿真,得到大量轨迹数据样本;提出CNN-LSTM神经网络的混合轨迹预测模型,并利用滑动窗口法和差分法构造输入输出的轨迹数据对,将预测问题转化为有监督的学习问题;将所提模型与LSTM神经网络模型、门控循环单元(GRU)神经网络模型和反向传播(BP)神经网络模型在同一数据集下进行仿真实验。研究结果表明,CNN-LSTM神经网络模型预测3s后的平均累积预测误差在x轴方向约为14.83m,y轴方向约为20.77m,z轴方向约为0.75m,且轨迹预测精度优于单一模型,为弹丸轨迹预测研究提供了一定的参考。
To solve the problem of nonlinear trajectory prediction of projectile, a novel hybrid trajectory prediction model based on convolutional neural network (CNN) and long and short-term memory (LSTM) neural network is proposed. A 6DOF projectile movement model is established, and a substantial dataset of trajectory samples is obtained through exterior ballistics simulations employing the four-order Runge-Kutta method. Secondly, the hybrid CNN-LSTM trajectory prediction model is proposed, and the input and output trajectory data pairs are constructed by using the sliding window method and first-order difference method, which transforms the prediction problem into a supervised learning problem. Then, the proposed model is compared with LSTM neural network model, gated recurrent unit (GRU) neural network model and back propagation (BP) neural network model using the same dataset. The results show that the average cumulative prediction error of CNN-LSTM model after 3s is about 14.83m in the x-axis direction, 20.77m in the y-axis direction and 0.75m in the z-axis direction. The trajectory prediction accuracy of CNN-LSTM neural network model is better than that of a single model, which provides valuable insights for advancing projectile trajectory prediction research. {{custom_citation.content}}
{{custom_citation.annotation}}
|
| [14] |
{{custom_citation.content}}
{{custom_citation.annotation}}
|
| [15] |
{{custom_citation.content}}
{{custom_citation.annotation}}
|
| [16] |
{{custom_citation.content}}
{{custom_citation.annotation}}
|
| [17] |
{{custom_citation.content}}
{{custom_citation.annotation}}
|
| [18] |
{{custom_citation.content}}
{{custom_citation.annotation}}
|
| [19] |
密俊霞, 于会龙, 席军强. 基于MLP-SVM的驾驶员换道行为预测[J]. 兵工学报, 2022, 43(12):3020-3029.
The uncertainty of human driver behavior brings challenges to the application of advanced driver assistance systems. In order to more accurately predict the lane-changing behavior of a driver, we studied the multi-layer perceptron (MLP) and the support vector machine (SVM), and designed the hybrid algorithm of MLP-SVM to predict the lane-changing behavior of the driver. Based on the vehicle information and the surrounding traffic environment information, the prediction model of driver's lane changing behavior is built. The real traffic dataset is used to verify the proposed model. The results show that compared with the prediction model of driver's lane changing behavior based on support vector machines or multi-layer perceptrons, the hybrid prediction model of driver's lane changing behavior achieves the highest prediction accuracy of 92.6%, and can predict the lane changing behavior earlier with the advanced prediction time up to 4.54 s.
{{custom_citation.content}}
{{custom_citation.annotation}}
|
| [20] |
{{custom_citation.content}}
{{custom_citation.annotation}}
|
| [21] |
{{custom_citation.content}}
{{custom_citation.annotation}}
|
| [22] |
徐庚, 何永旭, 张勇刚. 基于罗德里格斯参数的惯性系传递对准算法[J]. 系统工程与电子技术, 2022, 44(9):2903-2913.
针对传统的传递对准模型在大失准角下的强非线性问题以及由残余杆臂误差导致的传递对准精度下降问题, 提出了一种改进的惯性系传递对准算法。首先, 对子惯导姿态矩阵进行链式分解, 得到常值姿态矩阵; 然后, 利用罗德里格斯参数等价替代该常值姿态矩阵, 建立关于罗德里格斯参数和残余杆臂误差的具有弱非线性量测的传递对准模型; 最后, 利用非线性滤波对状态进行估计。基于摇摆运动的仿真实验表明, 在存在大安装误差角以及残余杆臂误差情况下, 算法相比于现有方法, 对准速度更快, 对准精度更高, 在5~10 s内即可完成传递对准。车载试验结果也间接说明算法具有更高的传递对准性能。
Aiming at the strong nonlinear problem for the conventional transfer alignment model with large misalignment angle and the problem of the degraded alignment accuracy induced by the residual lever arm error, an improved inertial-frame-based transfer alignment (ITA) method is proposed for inertial navigation system (INS). Firstly, a constant attitude matrix is obtained based on the chain rule for the attitude matrix of slave INS. Then, the constant attitude matrix is equivalently replaced by the Rodriguez parameter, and a novel transfer alignment model with weakly nonlinear measurement equation is established based on the Rodriguez parameter and the residual lever arm error. Finally, the nonlinear Kalman filters are implemented for the estimation. Simulation results under the sway motion illustrate that when the installation error angles are large and the residual lever arm error exists, the ITA method has the faster alignment speed and the better alignment accuracy than existing transfer alignment methods, and the transfer alignment can be completed in 5~10s. The field test results also illustrate that the ITA method has significantly better alignment performance. {{custom_citation.content}}
{{custom_citation.annotation}}
|
| [23] |
{{custom_citation.content}}
{{custom_citation.annotation}}
|
| [24] |
钱杏芳, 林瑞雄, 赵亚男. 导弹飞行力学[M]. 北京: 北京理工大学出版社, 2000.
{{custom_citation.content}}
{{custom_citation.annotation}}
|
| [25] |
{{custom_citation.content}}
{{custom_citation.annotation}}
|
| [26] |
Deep spiking neural networks (SNNs) offer the promise of low-power artificial intelligence. However, training deep SNNs from scratch or converting deep artificial neural networks to SNNs without loss of performance has been a challenge. Here we propose an exact mapping from a network with Rectified Linear Units (ReLUs) to an SNN that fires exactly one spike per neuron. For our constructive proof, we assume that an arbitrary multi-layer ReLU network with or without convolutional layers, batch normalization and max pooling layers was trained to high performance on some training set. Furthermore, we assume that we have access to a representative example of input data used during training and to the exact parameters (weights and biases) of the trained ReLU network. The mapping from deep ReLU networks to SNNs causes zero percent drop in accuracy on CIFAR10, CIFAR100 and the ImageNet-like data sets Places365 and PASS. More generally our work shows that an arbitrary deep ReLU network can be replaced by an energy-efficient single-spike neural network without any loss of performance.Copyright © 2023. Published by Elsevier Ltd.
{{custom_citation.content}}
{{custom_citation.annotation}}
|
| [27] |
杨观赐, 杨静, 李少波, 等. 基于Dopout与ADAM优化器的改进CNN算法[J]. 华中科技大学学报(自然科学版), 2018, 46(7):122-127.
{{custom_citation.content}}
{{custom_citation.annotation}}
|
| {{custom_ref.label}} |
{{custom_citation.content}}
{{custom_citation.annotation}}
|
PDF(7646 KB)
Collection(s)
Fig.1 Patriot missile launch process adapter separation[2]Fig.2 CNN structureFig.3 Schematic diagram of SVMFig.4 Flowchart of CNN-SVM-based adapter drop point predictionFig.5 Schematic diagram of adapter separation durimgr launchingFig.6 Illustration of coordinate system transformationFig.7 Adapter wind tunnel experiment under different angles of attackFig.8 Adapter separation experiment[25]Fig.9 Comparison of experimental drop point distributionsFig.10 Distribution density map of adapter drop points
Table 1 CNN model structural parametersFig.11 Predicted results of X-direction training set (R2=0.9968)Fig.12 Predicted results of Y-direction training set (R2=0.9977)Fig.13 Training set error analysis chartFig.14 Predicted results of X-direction training set (R2=0.9972)Fig.15 Predicted results of Y-direction training set (R2=0.9973)Fig.16 Test set error analysis chartTable 2 Initial conditions for Monte Carlo experimentFig.17 Result of Monte Carlo experimentFig.18 Box plot of Monte Carlo experimentFig.19 Solution speed comparisonFig.20 Solution speed comparison/
| 〈 |
|
〉 |
